1

how to calculate that the second homology group for orientable surface of genus $g$ is $\mathbb{Z}$?

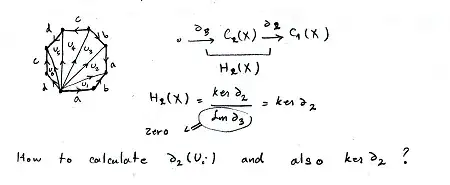
by calculating I mean that find $ker \partial_2$ in chain complex,for example for torus of two hole: enter image description here

also I know that the first homology group is $\mathbb{Z}^{2g}$ but except torus with one hole I can't do its calculation.

I can think geometrically about that as I study Intuition of the meaning of homology groups but one time I want to see its calculation,also I have the same problem with non-orientable one.for $\mathbb{RP}^2$ and klein bottle I know the algebrical works,but more than it I couldn't go far.

any hint or references will be great,thanks a lot.

Community
  • 1
kpax
  • 2,911

2 Answers2

2

I think this is easiest to see using cellular homology. There is only one $2$-cell $U$, so $C_2 \cong \mathbb{Z}$. The boundary of this $2$-cell is the product of the commutators of the $2g$ $1$-cells: $[a_1, b_1] \cdots [a_g, b_g]$ where $[a_i, b_i] = {a_i}^{-1} {b_i}^{-1} a_i b_i$. For instance, if you traverse the boundary of the octagon you've drawn to represent a genus $2$ surface, you'll see that we traverse each edge twice, once in the positive direction, and once in the negative direction. See here for a reference. However, since the homology groups are abelian groups, these commutators are trivial, i.e., $$ \partial_2(U) = -a_1 - b_1 + a_1 + b_1 + \cdots + -a_g - b_g + a_g + b_g = 0 \, . $$ Since $\partial_2$ maps the generator of $C_2$ to $0$, then $\partial_2 = 0$, hence $\ker \partial_2 = C_2 \cong \mathbb{Z}$.

Viktor Vaughn
  • 19,278
  • I think my problem is that I still don't study cellular homology,but thanks for making me aware of this. – kpax May 01 '14 at 06:18
  • Ah, I should have noticed that you had drawn in simplices. I'll think some more if there's an easy way to see this for simiplicial homology. One of the advantages of cellular over simplicial homology is that you can get away with much smaller chain groups---that's why I prefer it. – Viktor Vaughn May 01 '14 at 15:05
1

I highly recommend Allen Hatcher's Algebraic Topology if you haven't read it yet. It's available for free, and it's an extremely good reference.

For your question, I refer you to the picture on page 105 of the book. It should clarify a lot of things. I'm assuming you're using simplicial homology, considering the picture you've drawn. Here you should label the "intermediate" edges (there are five of them), let's say $x_1, \dots, x_5$ from left to right. Then for example $\partial_2 v_0 = x_1 - c - d$. Similarly you should compute $\partial_2 v_k$ for every $k$; then it's simply a matter of computing the kernel of a linear transformation given the image of a basis. Writing down the matrices should help.

Of course, if you aren't afraid to get fancy (this probably won't make sense to you right now but I'll include it for the sake of completeness): this is a compact manifold of dimension two, and it's orientable, therefore its second homology group is $\mathbb{Z}$. The projective plane and the Klein bottle aren't orientable, so their second homology group is zero.

Najib Idrissi
  • 54,185