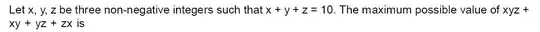
I have tried am-gm inequality,i am getting that $xyz$ is greater than $36.9$.
I tried hit and trial,but it is of no use also.
Could anyone give a definite process?
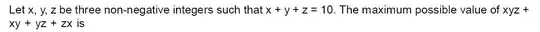
I have tried am-gm inequality,i am getting that $xyz$ is greater than $36.9$.
I tried hit and trial,but it is of no use also.
Could anyone give a definite process?
Hint: $x+1+y+1+z+1=13$
Bound $(x+1)(y+1)(z+1)$ from above using AM-GM.
Hence maximum is $(13/3)^3-11$ and occurs when $x=y=z$.
$xyz+xy+yz+zx=xyz~\bigg(1+\dfrac1x+\dfrac1y+\dfrac1z\bigg)$, but the harmonic mean of the three variables is $H=\dfrac3{\dfrac1x+\dfrac1y+\dfrac1z}\iff\dfrac1x+\dfrac1y+\dfrac1z=\dfrac3H$ . At the same time, $A>G>H$, with $A=\dfrac{10}3$ and
$G=\sqrt[3]{xyz}~=>$ we are left with maximizing $G^3\bigg(1+\dfrac3H\bigg)\geqslant G^3\bigg(1+\dfrac3G\bigg)$, which lower bound peaks for $G_\text{max}=A=\dfrac{10}3$ , which only happens when $x=y=z$. Since the three variables are integers, the solutions obtained by rounding are $3,3$, and $4$, for which we have a maximum of $69$, which is just shy of the global maximum $\dfrac{1900}{3^3}\approx70.37$, obtained for $x=y=z=3\dfrac13\cdot$ QED.