5

I have no idea whether this is known or not and I couldn't find anything related on Google. While I was studying , I come up with this idea $1+n!=m^{2} $ for some $n,m\in\mathbb{N}$

$1+4!=5^{2}$

$1+5!=11^{2}$

$1+?!=?^{2}$

and the question is what is the next number? Wolfram Alpha gave me this interesting graph: 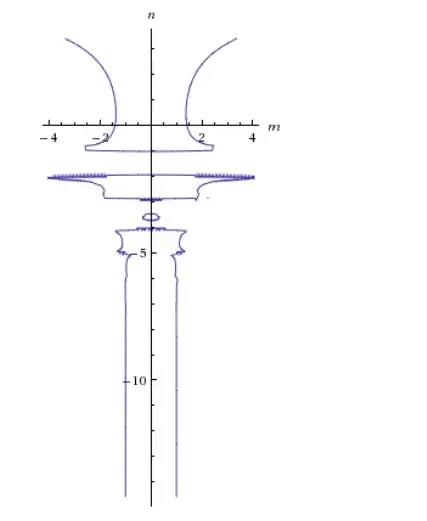enter image description here

Thanks in advance for your interest.

Martin Sleziak
  • 53,687
Airbag
  • 403

2 Answers2

7

$$4!+1=5^2\\5!+1=11^2\\7!+1=71^2$$

This problem is known as Brocard's Problem, and pairs of integers which satisfy it are known as Brown Numbers. There are no other known solutions up to $10^9!+1$.

user137794
  • 2,469
-2

$m^2-n!-1=0\Rightarrow m=\pm\sqrt{(n!)^2+1}$ this should help you to find $n$ since you need $(n!)^2+1$ to be a square I.e. $(n!)^2+1=a^2$ for some $a\in(2k-1)\mathbb{N}$ (odds)

Ellya
  • 11,783
  • I don't think this is easy because here $\Gamma(n+1)^{2}+1=a^{2}$ but original questions is $\Gamma(n+1) + 1=m^{2}$. Am I wrong ? – Airbag Apr 24 '14 at 16:23