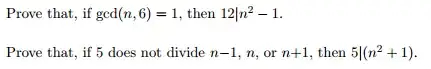
I need help proving the first one via Fermat's little theorem.
I need a hint, or a good starter!
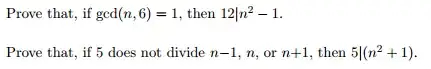
I need help proving the first one via Fermat's little theorem.
I need a hint, or a good starter!
Just notice that if it works for $n$ it also works for $n+6$ and $n-6$, so it is enough to prove the theorem for $n \in \{0,1,2,3,4,5\}$.