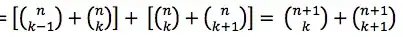$$\left[\binom n{k-1} + \binom nk\right] + \left[\binom nk + \binom n{k+1}\right] = \binom{n+1}k + \binom{n+1}{k+1}$$
Can anyone else explain to me, without using Pascal's triangle, how this addition works?. I don't know how to add [C(n,k-1) + C(n, k)] + [C(n,k) + C(n,k+1) yields C(n+1,k) + C(n+1, k+1).
Thanks
The identity $\binom{m}{r-1}+\binom{n}{r}=\binom{n+1}{r}$ can be obtained in various ways. In my opinion the nicest approach is combinatorial.
We have a group of $n+1$ people, including Alicia. How many ways are there to choose a committee of $r$ people from this group?
By definition, there are $\binom{n+1}{r}$ ways to do the job.
Let us count the number of committees another way. There are two types of committee of $r$ people, (i) the ones that contain Alicia and (ii) the ones that don't.
There are $\binom{n}{r-1}$ committees of $r$ that contain Alicia, for we need to choose $r-1$ people to join her.
There are $\binom{n}{r}$ committees of $r$ that do not contain Alicia, for we must choose $r$ non-Alicias to form the committee.
We have counted the same thing in two different ways, so the answers must be the same. It follows that $\binom{n+1}{r}=\binom{n}{r-1}+\binom{n}{r}$.
The result of the OP comes from applying the above result twice, once with $n$ and $k$, and the second time with $n$ and $k+1$. Note that the expression obtained can be further simplified to $\binom{n+2}{k+1}$.
Remark: We can also prove the result mechanically using the formula $\binom{m}{k}=\frac{m!}{k!(m-k)!}$. For $$\binom{n}{r-1}=\frac{n!}{(r-1)!(n-r+1)!}=\frac{n!}{r!(n-r)!}\frac{r}{n-r+1}.$$ and $$\binom{n}{r}=\frac{n!}{r!(n-r)!}.$$ Add. We get $$\binom{n}{r-1}+\binom{n}{r}=\frac{n!}{r!(n-r)!}\left(\frac{r}{n-r+1}+1\right)=\frac{n!}{r!(n-r)!}\cdot\frac{n+1}{n-r+1}.$$ But the right-hand side above is equal to $\frac{(n+1)!}{r!(n-r+1)!}$, which is $\binom{n+1}{r}$.
