4

Find $x$ in the following equation: $$3^x+x^3=17$$

user2345215
  • 16,422
voca
  • 141

4 Answers4

5

I will only give you a hint since this is a homework assignment. Try these numbers $-3, -2, -1, 0, 1, 2,3$. Are any of these a solution?

If you find one, try to show that this is the only solution. This you can do by considering the derivative of $f(x) = 3^x + x^3$: $$ f'(x) = ... $$ If you can show that this derivative is strictly positive or strictly negative, then you have shown that the function is strictly increasing (or strictly decreasing). Then it can only have one solution (you might have to think about why this would be true).

J. W. Tanner
  • 60,406
Thomas
  • 43,555
  • 1
    +1, but you don't need calculus to show that it's strictly increasing; both of the functions $3^x$ and $x^3$ are manifestly increasing over their domains, and so their sum is as well. – Steven Stadnicki Apr 21 '14 at 17:54
  • @StevenStadnicki: I agree that it is "obvious", but his teacher might still want him to show this. – Thomas Apr 21 '14 at 17:55
  • 1
    @Thomas Certainly - but again, I wouldn't use calculus to do it. $3^{x+h} = 3^x3^h \gt 3^x$ if $h\gt 0$, and similarly (if a little more complicatedly) for the other term. – Steven Stadnicki Apr 21 '14 at 17:57
  • @StevenStadnicki: I agree. – Thomas Apr 21 '14 at 17:58
  • 3^x + x^3 = 17 then 3^x + x^3 =3^2 + 2^3 then compare we deduce that x must be 2.@Thomas.@ Steven Stadnicki – voca Apr 21 '14 at 17:58
  • My Question is to find x only not prove. – voca Apr 21 '14 at 18:01
  • @mol: You want to find $x$. You find one value of $x$ that solves the equation, but in the statement "Find $x$ ..." it is implied that you have to find all $x$. So the question for this specific equation becomes: How can I prove/show that this one solution that I have found is the only solution. – Thomas Apr 21 '14 at 18:03
  • @ Thomas : is this is true ? 3^x + x^3 = 17 then 3^x + x^3 =3^2 + 2^3 then compare we deduce that x must be 2..@ – voca Apr 21 '14 at 18:05
  • @mol: Yes and No. You end up finding the only solution, but you haven't argued why $2$ is the only solution. So no it would not be correct in the sense that you need to say more. – Thomas Apr 21 '14 at 18:06
  • ...the only solution among real numbers. – DanielV Apr 21 '14 at 19:55
2

Or, compute the derivative and note that it is always $ > 0$. Then by Rolle's there is at most one solution. (It is easy to guess our solution...)

Sandeep Silwal
  • 8,135
1

Note that if $y\gt 0$we have $3^y\gt 1$ so that if $x\ge 0$ $$3^{x+y}+(x+y)^3=3^x\cdot 3^y +x^3+(3x^2y+3xy^2+y^3)\gt 3^x+x^3$$

And it is very easy to show that for $x\le 0$ we have $3^x+x^3\le 1+0\lt 17$

So the function is increasing for positive $x$ (without calculus) and there is at most a single solution.

Mark Bennet
  • 100,194
1

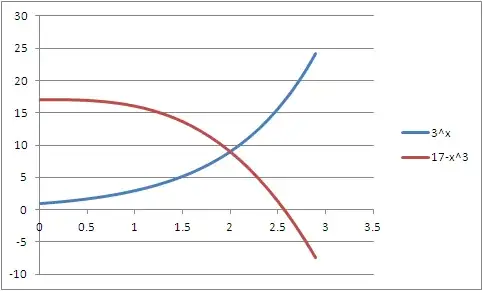
Please draw functions 3^x and 17-x^3. By looking at the picture, you can see there is only one solution. Others have already proved that using basic computations. Then you can bound your answer and check the value that makes this equation true is x=2.

enter image description here

JLBarba
  • 9