Last fall, I wrote up a proof that $\cos(36^\circ) = \varphi/2$ for an undergraduate trigonometry class. As my proof is different from the others provided (while it is similar substantially similar to evilman999's argument, my argument is a bit more verbose, and I think that my picture is better ), and since this question has been asked again, I thought it reasonable to add my own two cents. I will note that this isn't an exact answer for the question asked above (which outlines a specific strategy), but that this answer is appropriate for the more abstract question "How do we prove that $\cos(36^\circ) = \varphi/2$?"
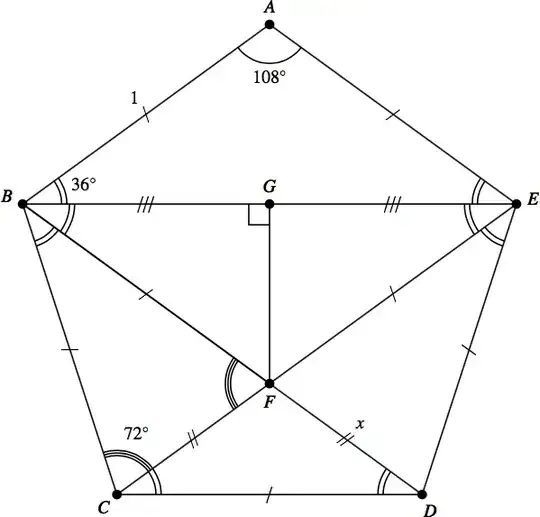
Let $ABCDE$ be a regular pentagon, where it may assumed without loss of generality that the sides are of unit length. The triangle $\triangle ABE$ is isosceles with $\measuredangle BAE = 108^\circ$ (this is the measure of each angle in a regular pentagon), which implies that
\begin{equation*}
\measuredangle ABE = \measuredangle AEB = 36^\circ.
\end{equation*}
By similar arguments,
\begin{equation*}
\measuredangle CBD
= \measuredangle DEC
= \measuredangle DCE
= \measuredangle CDB
= 36^\circ.
\end{equation*}
Next, observe that the measures of the three angles formed by the diagonals emanating from $B$ must sum to $108^\circ$. This implies that
\begin{equation*}
\measuredangle DBE
= 108^\circ - 2\cdot 36^\circ
= 36^\circ.
\end{equation*}
Similarly, $\measuredangle CEB = 36^\circ$.
Let $F$ denote the intersection of the diagonals $\overline{BD}$ and $\overline{EC}$. By the angle-angle similarity theorem, $\triangle BEF \sim \triangle DCF$. The goal now is to use this similarity to determine the length of $\overline{BE}$. Note that
\begin{equation*}
\measuredangle BCF + \measuredangle FCD = \measuredangle BCF + 36^\circ = 108^\circ
\implies \measuredangle BCF = 72^\circ.
\end{equation*}
As the angle sum of a triangle is $180^\circ$, it follows that $\measuredangle BFC = 72^\circ$, and so $\triangle BCF$ is isosceles. But then $\overline{BC} \cong \overline{BF}$. In particular, this implies that $\overline{BF}$ is of unit length.
Let $x$ denote the length of $\overline{FD}$, so that the length of $\overline{BD}$ is $1+x$. Then, as all of the diagonals in the regular pentagon $ABCDE$ are congruent, the length of $\overline{BE}$ must also be $1+x$. By properties of similar triangles,
\begin{equation*}
\frac{\ell(\overline{BE})}{\ell(\overline{BF})}
= \frac{\ell(\overline{DC})}{\ell(\overline{DF})}
\implies \frac{1+x}{1} = \frac{1}{x}
\implies x^2 + x - 1 = 0
\implies x = \frac{-1+\sqrt{5}}{2}.
\end{equation*}
Let $G$ denote the midpoint of $\overline{BE}$, and observe that $\overline{FG}$ is perpendicular to $\overline{BG}$. Using properties of right-triangles (specifically, using thhe right-triangle definitions of the trigonometry functions, i.e. "SOH-CAH-TOA") and the earlier observation that $\measuredangle DBE = 36^\circ$, it is now possible to conclude that
\begin{equation*}
\cos(36^\circ)
= \frac{\ell(\overline{BG})}{\ell(\overline{BF})}
= \frac{\frac{1}{2}(x+1)}{1}
= \frac{1}{2}\left( \frac{-1+\sqrt{5}}{2} + 1 \right)
= \frac{1+\sqrt{5}}{4} = \frac{\varphi}{2},
\end{equation*}
where $\varphi$ is the golden ratio.


