Cycloidal coincidence?

Question

For the cycloid $$x=a(t-\sin t)\ ,\quad y=a(1-\cos t)$$ we have, as is easily seen, $$\frac{dx}{dt}=y\ .$$ Does this have any geometrical or physical significance? Or is it just a meaningless coincidence?

Edit: please note that I'm not asking about the algebra - I can do the algebra. Nor do I just want the algebra restated in words.

I don't want to derail any potential answers and for this reason I hesitate to be too directive, but what I would like to see might be something like this: the geometric meaning of $\frac{dx}{dt}$ is . . . , and the geometric meaning of $y$ is . . . , and these are the same because . . .

Another possible approach: is there anything worthwhile that can be said in general about a curve of the form $$x=f(t)\ ,\quad y=f'(t)\ .$$

Answer 1

Suppose $r$ is the radius of the circle and $\theta$ is the angle (measured counter-clockwise from the positive x-axis as usual) at which the radius is pointing at time $t$. Note that the point is travelling clockwise.

If the angular speed is $1\text{rad}/\text{(time unit)}$ then the speed at the perimeter is $r\,\text{rad}/\text{(time unit)}$. Thus a small perturbation in time $t$ will result in a change of $\Delta r(\cos\theta,\sin\theta)$ due to angular change and $(r\Delta t,0)$ due to the motion of the center point. Also we have $\frac{d\theta}{dt}=-1$.

The net change in the point will then be $$r\left(\frac{d}{dt}\cos\theta,\frac{d}{dt}\sin\theta\right)\Delta t+(r\Delta t,0)=r(\sin\theta+1,-\cos\theta)\Delta t$$ Therefore the rate of change of $x$ is $$\frac{\Delta x}{\Delta t}=\frac{r(\sin\theta+1)\Delta t}{\Delta t}=r(\sin\theta+1)$$ in the limit. But $y=r+r\sin\theta$ so $$\frac{dx}{dt}=y$$

Note that $$\theta=-{\pi\over 2}-t$$ where $t$ starts at $0$, for clarification. This, incidentally, shows that $$\bigg(x'(t),y'(t)\bigg)=r\left(\sin\left(-{\pi\over 2}-t\right)+1,-\cos\left(-{\pi\over 2}-t\right)\right)=r(-\cos t+1,\sin t)$$ so by integration we get $$(x(t),y(t))=\bigg(r(t-\sin t),r(-\cos t+1)\bigg)$$ after determining constants.

Answer 2

It's a very interesting observation, and I would imagine it's certainly not a meaningless coincidence. I'm sure someone else can give you a better description, but I think the "rolling ball" perspective suggests why such a relationship exists.

It turns out it's convenient to think of the change of position of the particle in the $x$ direction as coming fron two sources: The motion of the particle with respect to the center of the circle, and the motion of the center of the circle with respect to a stationary observer (See the image below, these are the two green arrows). So, we add these two speeds together, and we we have $\frac{d\ x}{d\ t}$. The center of the rolling ball is given by $(rt,r)$ and is always contributing velocity $\langle r, 0\rangle$ to the particle.

Now, it will be nice to have the angular speed, so we can find the linear speed of the point (all of this with respect to the center of the circle). Of course, when $t = 2\pi$, the $y$-coordinate is back to zero, so the angular speed is simply $1,$ and in turn the linear speed is simply $r$ (I'm calling the radius $r$, but it appears that you're using $a$). To simplify matters, I'll pretend $r=1$ from here on out.

The linear velocity is tangent to the circle, and we have this picture:

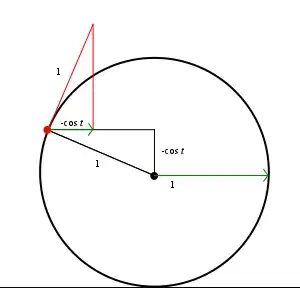
It's not too hard to label relevant pieces of the black, central triangle. Of course the radius (hypotenuse) is just $1,$ while the length of the vertical leg is $\ -\cos t$. This is because the top endpoint of the vertical leg has the same $y$-coordinate as the particle, which is $1-\cos t$. Thus we have broken the $y$-coordinate into two pieces: the radius of the ball, and the length of the vertical leg.

This, in turn, helps us start labeling pieces of the red triangle. Since the linear velocity is perpendicular to the radius of the ball and has magnitude $1,$ the red triangle is congruent to the black triangle. Thus, we see that the $x$-component of the linear velocity is also $\ -\cos t$.

Thus, adding the linear speed of the point (with respect to the center of the ball), $-\cos t$, to the linear speed of the center of the ball, $1,$ we get exactly what you want: $\frac{d\ x}{d\ t} = 1 -\cos t = y$.

I'm sure there's a more elegant argument, but it really is quite believable (staring at the rolling ball image) that the change in $x$ is, at the very least, proportional the the height of the point: when $y$ is near zero, the point moves mostly vertically, and when $y$ is near its maximum, the point moves mostly horizontally.

Great question, I hadn't seen this before, and it was quite fun figuring out what's going on!

---

Rolling cycloid image courtesy of Wikipedia. If I've committed some sort of image faux-pas (animated gif, or using the image directly), feel free to edit this post.