6

A 5 pointed star is inscribed in a circle of radius $r$.

Prove that the area of the star is $$ \frac{10 \tan\left(\tfrac{\pi}{10}\right)}{3-\tan^2\left(\tfrac{\pi}{10}\right)} r^2 $$

Sasha
  • 70,631
Rudstar
  • 1,173

1 Answers1

10

Consider the following diagram of the 5-pointed star:

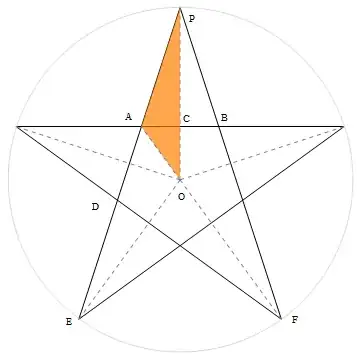
enter image description here

Clearly the area of the 5-star is $10$ times the area of the orange-shaded triangle $\triangle OAP$ which, in turn, equals half the height times the base: $$ A\left(\triangle OAP\right) = \tfrac{1}{2} \bar{AC} \cdot \bar{OP} = \tfrac{1}{2} \bar{AC} \cdot r $$ To find $\bar{AC}$ notice that it is a joint side of two right triangles, $\triangle OAC$ and $\triangle PAC$, hence $$ \bar{OC} = \frac{\bar{AC}}{\tan\left(\angle AOC\right)} \qquad \bar{PC} = \frac{\bar{AC}}{\tan\left(\angle APC\right)} = r - \bar{OC} \tag{1} $$

By the symmetry $\angle EOF = \tfrac{2}{5} \pi$, and $\angle AOB = \tfrac{2}{5} \pi$, and hence $\angle AOC = \tfrac{1}{2} \angle AOB = \tfrac{1}{5} \pi$. By the inscribed angle theorem applied to angle $\angle EPF$, $$ \angle APF \equiv \angle EPF = \frac{1}{2} \angle EOF = \frac{\pi}{5} \quad \therefore \quad \angle APC = \tfrac{1}{2} \angle APF = \frac{\pi}{10} $$ Using these angles in eq. $(1)$: $$ r = \frac{\bar{AC}}{\tan\left(\tfrac{1}{5} \pi \right)} + \frac{\bar{AC}}{\tan\left(\tfrac{1}{10} \pi \right)} $$ and solving for $\bar{AC}$ we get $$ A\left(\triangle OAP\right) = r^2 \cdot \frac{1}{2} \frac{1}{\frac{1}{\tan\left(\tfrac{1}{5} \pi \right)} + \frac{1}{\tan\left(\tfrac{1}{10} \pi \right)}} = r^2 \frac{ \tan\left(\frac{\pi}{5}\right) \tan\left(\frac{\pi}{10}\right)}{2 \left(\tan\left(\frac{\pi}{5}\right) + \left(\frac{\pi}{10}\right)\right)} \tag{2} $$ Furthermore, using angle doubling formula for tangent in the previous eq. $(2)$: $$ \tan\left(\frac{\pi}{5}\right) = \frac{2 \tan\left(\frac{\pi}{10}\right)}{1 - \tan^2\left(\frac{\pi}{10}\right)} $$ we have $$ A\left(\triangle OAP\right) = r^2 \frac{\tan\left(\frac{\pi}{10}\right)}{3- \tan^2\left(\frac{\pi}{10}\right)} $$ We finish by recalling the area of the 5-star equals 10 times the area of $\triangle AOP$: $$ A\left({\huge \star}\right) = \frac{10 \cdot \tan\left(\frac{\pi}{10}\right)}{3- \tan^2\left(\frac{\pi}{10}\right)} r^2 $$

Sasha
  • 70,631