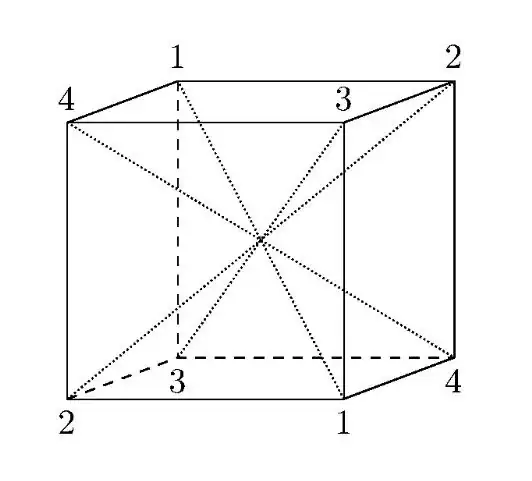
Let's imagine a die with faces numbered 1 through 6.
First of all, a cube has six faces, so $|G|$ divides $6! = 720$ .
However, our flips need to preserve pairs of opposite faces (which must add up to 7).
That means once we know where faces 1, 2, and 3 are sent, we've completely determined what happens to the die.
One can be sent anywhere, two can be send to the remaining four places, and three can be sent to the remaining two places.
So, we get $6 * 4 * 2 = 48$.
However, half of those transformations change the chirality of the die and do not correspond to rigid motions in $\mathbb{R}^3$, so we get
$$ 48 / 2 = 24 $$
We can prove that the group of rigid motions that preserve a cube is isomorphic to $S_4$ by establishing an isomorphism between two-line notation on four elements and plus-minus two-line notation on three elements, with an even number of minus signs.
I haven't seen plus-minus two-line notation before; it's something I made up for the purposes of this problem. We're really just decorating the bottom row with coefficients drawn from the group $\{-1, +1\}$ and saying those coefficients commute with everything when composing two plus-minus permutations given in tabular form.
Here's a permutation of $\{a, b, c, d\}$.
$$ \begin{pmatrix} a & b & c & d \\ b & c & a & d \end{pmatrix} $$
Here's the corresponding plus-minus permutation of $\{a, b, c\}$.
$$ \begin{pmatrix} a & b & c \\ +b & +c & +a \end{pmatrix} $$
Here's another permutation of $\{a, b, c, d\}$. This time it doesn't fix $d$.
$$ \begin{pmatrix} a & b & c & d \\ d & b & c & a \end{pmatrix} $$
Here's the corresponding plus-minus permutation of $\{a, b, c\}$
$$ \begin{pmatrix} a & b & c \\ +a & -c & -b \end{pmatrix} $$
In the original permutation $a$ is sent to $d$, so $d$ is replaced with $a$. $b$ and $c$ each get a minus sign and get swapped. $a$ gets a $+$ sign.
So, more generally, here's the map $\varphi$.
Let $\pi$ be a permutation of $\{a, b, c, d\}$.
If $\pi$ fixes $d$, $\varphi(\pi)$ sends each $x$ among $a, b, c$ to $+\pi(x)$.
If $\pi$ does not fix $d$, $\varphi(\pi)$ sends $\pi^{-1}(d)$ to $+z$ with $z$ being the sole element $\{a, b, c\} \setminus \pi(\{a, b, c\})$. $\varphi$ swaps and negates the remaining elements.
We invert $\varphi$ by noting the number of minus signs in our plus-minus permutation of $\{a, b, c\}$. If it is $0$, we add another row sending $d$ to $d$.
If it is nonzero, we find the single row with a positive entry, exchange that entry and $d$ in the bottom row, and then remove all the plus signs and minus signs and swap the two entries that had minus signs.
Definition of inverse in two-line notation.
You exchange the top and bottom rows.
$$ \begin{pmatrix} a & b & c & d \\ b & c & a & d \end{pmatrix} $$
This becomes
$$ \begin{pmatrix} b & c & a & d \\ a & b & c & d \end{pmatrix} $$
Which normalizes to
$$ \begin{pmatrix} a & b & c & d \\ a & c & b & d \end{pmatrix} $$
Definition of inverse in signed two line notation.
You exchange the top and bottom rows, and then move the signs to the bottom (this only works because in the group $\{-1, 1\}$, all the elements are involutions).
$$ \begin{pmatrix} a & b & c \\ +b & +c & +a \end{pmatrix} $$
Becomes
$$ \begin{pmatrix} +b & +c & +a \\ a & b & c \end{pmatrix} $$
Becomes
$$ \begin{pmatrix} b & c & a \\ +a & +b & +c \end{pmatrix} $$
Which normalizes to
$$ \begin{pmatrix} a & b & c \\ +c & +a & +b \end{pmatrix} $$
Lemma 51: $\varphi$ is a bijection.
Start off with a two-line permutation of $\{a,b,c,d\}$, $\pi$.
Suppose $\pi$ fixed $d$. $\varphi(\varphi(\pi))$ is equal to $\pi$, since we add in $+$ signs and then remove them in the first three columns and $d$ is fixed.
Suppose $\pi$ does not fix $d$. Suppose without loss of generality that $\pi(a) = d$. $b$ and $c$ will be sent to negative letters and $a$ will be sent to the sole positive letter. The sole positive entry in the second row of $\varphi(\pi)$ will be sent back to $d$ in $\varphi(\varphi(\pi))$. The other entries will be translated correctly. Additionally the $d$ column will get the remaining letter.
Since the domain and codomain of $\varphi$ are both finite, $\varphi$ is a bijection.
Lemma 101: $\varphi$ is an injective group homomorphism and hence an isomorphism.
The identity element $\begin{pmatrix} a & b & c & d \\ a & b & c & d \end{pmatrix}$ is sent to the identity element $\begin{pmatrix} a & b & c \\ +a & +b & +c \end{pmatrix}$.
Let $\pi$ be a permutation of $\{a, b, c, d\}$. $\varphi(\pi^{-1})$ is equal to $\varphi(\pi)^{-1}$.
Suppose $\pi$ fixes $d$. Adding $+$ signs to the bottom row and removing the last row, as an action, commutes with swapping the rows and renormalizing, as an action.
Suppose $\pi$ does not fix $d$.
$\pi$ has the form $\begin{pmatrix} a & b & c & d \\ \pi(a) & \pi(b) & \pi(c) & \pi(d) \end{pmatrix}$
We can perform the transformation operation on the entire full table without removing the column immediately. Let $\varphi(\pi, x)$ mean $\varphi(\pi)(x)$, but look nicer.
$$ \begin{pmatrix} a & b & c & d \\ \varphi(\pi, a) & \varphi(\pi, b) & \varphi(\pi, c) & \varphi(\pi, d) \end{pmatrix} $$
Let $\varphi(\pi, d)$ be $+d$ always.
From this form, it should be clear that performing the inverse and renormalizing commutes with removing the last column.
Now, I'll cover composition in general.
First, I observe without explicit proof that $\varphi$ is a homomorphism when restricted to permutations of $\{a,b,c,d\}$ that fix $d$.
Let $\tau$ be a transposition involving $d$.
I will now prove that $(\pi\tau)^\varphi = \pi^\varphi\tau^\varphi$, note that $fg$ is equivalent to $g \circ f$ in function notation.
Suppose without loss of generality that $\tau$ exchanges $a$ and $d$.
$$ \tau^\varphi = \begin{pmatrix} a & b & c \\ +a & -c & -b \end{pmatrix} $$
Let suppose $\pi$ fixes $d$.
This leaves six possible permutations
- $ \begin{pmatrix} a & b & c & d \\ a & b & c & d \end{pmatrix} $
- $ \begin{pmatrix} a & b & c & d \\ a & c & b & d \end{pmatrix} $
- $ \begin{pmatrix} a & b & c & d \\ b & a & c & d \end{pmatrix} $
- $ \begin{pmatrix} a & b & c & d \\ b & c & a & d \end{pmatrix} $
- $ \begin{pmatrix} a & b & c & d \\ c & a & b & d \end{pmatrix} $
- $ \begin{pmatrix} a & b & c & d \\ c & b & a & d \end{pmatrix} $
For each of these, we check the theorem by hand.
I'll check case #5 explicitly.
$$ \begin{pmatrix} a & b & c & d \\ c & a & b & d \end{pmatrix}^\varphi \begin{pmatrix} a & b & c & d \\ d & b & c & a \end{pmatrix}^\varphi \;\;\text{equals} \\
\begin{pmatrix} a & b & c \\ +c & +a & +b \end{pmatrix} \begin{pmatrix} a & b & c \\ +a & -c & -b \end{pmatrix} \;\; \text{equals} \\
\begin{pmatrix} a & b & c \\ -b & +a & -c \end{pmatrix} \;\;\text{equals} \\
\begin{pmatrix} a & b & c & d \\ c & d & b & a \end{pmatrix}^\varphi \;\; \text{as desired}
$$
We chose the transposition to involve $a$ arbitrarily at the beginning, so we're done.
Thus, as desired, the symmetries of a cube as a group are isomorphic to $S_4$