Why do some series converge and others diverge?

Question

Why do some series converge and others diverge; what is the intuition behind this? For example, why does the harmonic series diverge, but the series concerning the Basel Problem converges?

To elaborate, it seems that if you add an infinite number of terms together, the sum should be infinite. Rather, some sums with an infinite number of terms do not add to infinity. Why is it that adding an infinite number of terms sometimes results in an answer that is finite? Why would the series of a partial sum get arbitrarily close to a particular value rather than just diverge?

Answer 1

A series converges if the partial sums get arbitrarily close to a particular value. This value is known as the sum of the series. For instance, for the series $$\sum_{n=0}^\infty 2^{-n},$$ the sum of the first $m$ terms is $s_m = 2-2^{-m+1}$ (you can figure this out using the fact $1+x+x^2+\cdots+x^n = (x^{n+1}-1)/(x-1)$). Since $s_m$ tends to $2$ in the limit as $m$ gets large, the sum is $2$. In this case we can represent the partial sums as a formula and think of it as a limit. If you need a visualization, consider the following image from this thread.

It turns out that if $\sum_{n=0}^\infty a_n$ converges, we must have $a_n \to 0$ as $n \to \infty$. But just because $a_n$ goes to 0 doesn't mean the sum converges.

For instance, the partial sums of $\sum_{n=0}^\infty \frac{1}{n}$ go to infinity even though $1/n \to 0$ as $n \to \infty$. Look up the integral test or questions about the divergence of the harmonic series to learn why.

On the other hand, the series $\sum_{n=0}^\infty \frac{1}{n^2}$ does converge, to $\pi^2/6$, in fact. We can show that it converges using various theorems, one of them includes the integral test. To find the value of the sum requires more work.

So at the end of the day, we have to use specific tools to show specific series either converge or diverge. There's no complete algorithm for figuring this out that is taught (or even exists as far as I know).

Answer 2

Here's an intuitive answer

When a series converge it's because that the series goes towards a target, its limit. Likewise a diverging series has no target, it either jumps around in circles or goes to an infinite value. The harmonic series diverges because, even though it increases by smaller and smaller amounts, it will still never actually end at a target, basically for any value n there is some iteration of the harmonic series which has a larger value than that. It just flies away.

Answer 3

Maybe the best way to try to answer your question is in terms of theorems. For example, if you have an alternating series of decreasing terms that go to $0$ then the series clearly converges because the remainder after you add the first $n$ terms is bounded by the $n+1$th term. If you have a series of positive decreasing terms $a_n$, then there is a theorem that says that $\sum_n a_n$ converges if and only if $\sum_k 2^k a_{2^k}$ converges, which shows very clearly why the harmonic series diverges because for $a_n = 1/n$ you get $2^k a_{2^k} = 1$ and $1 + 1 + 1 + \ldots$ clearly diverges. Also the root test and ratio test explain why some series converge or diverge, by comparison to geometric series whose convergence and divergence you can basically take as an axiom when you are talking about why arbitrary series converge or diverge.

Answer 4

This answer is hopefully to increase your intuition about summation. Imagine adding infinitely many (non negative, for simplicity) numbers together. Roughly speaking, if this addition adds up to a finite number, you say that the series (the terms you are summing together) converges, and if it doesn't, you say that it diverges. This is just a natural generalisation of finite addition to infinitely many terms. Lets look at this a little more closer.

• For example, add the number $1$ to itself infinitely often. The result can not be anything finite, can it? So we say that the series $\sum_{n=1}^{\infty}1$ diverges.

• Consider then adding the numbers $1, \frac{1}{2}, \frac{1}{4},\frac{1}{8},...$ together. It turns out that they sum up to a finite number, which means that the series $\sum_{n=1}^{\infty}\frac{1}{2^{n}}$ converges. (In fact, the value of this sum equals $1$)

• What about if we add $1, \frac{1}{2}, \frac{1}{3},\frac{1}{4},...$ together? It turns out that these numbers don't add up to a finite number, in other words the series $\sum_{n=1}^{\infty}\frac{1}{n}$ diverges.

So it makes sense that in order for the series $\sum_{n=1}^{\infty}a_{n}$ for non-negative terms $a_{n}\in\mathbb{R}$ to converge, we must have $\lim_{n\to\infty}a_{n}= 0$. But is this enough? The answer is no, as we saw in the example above. But it turns out that if $a_{n}\to 0$ fast enough, then the given series $\sum_{n=1}^{\infty}a_{n}$ converges. For example, the sequence $(\frac{1}{2^{n}})_{n=1}^{\infty}$ converges to $0$ much more rapidly than the sequence $(\frac{1}{n})_{n=1}^{\infty}$.

To verify that the above example series add up to a finite number or not, you can use some known integral or convergence tests.

Answer 5

[I]f you add an infinite number of terms together, the sum should be infinite. Rather, some sums with an infinite number of terms do not add to infinity. Why is it that adding an infinite number of terms sometimes results in an answer that is finite? Why would the series of a partial sum get arbitrarily close to a particular value rather than just diverge?

In the hope this long-belated musing helps, let's come at the question from the opposite direction. Suppose you take a (finite) positive real number $T$ (for total): $1$, or $\pi^{2}/6$, or whatever.

Can you partition this number into infinitely many positive summands?

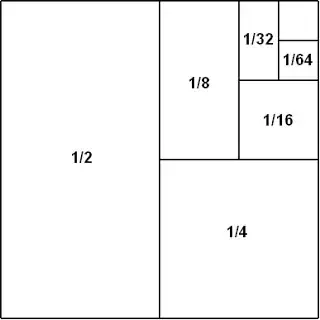
Perhaps it's clear(er) the answer is "yes". Metaphorically, if you start with a piece of licorice (or chocolate-covered spaghetti, or Pocky, which is basically chocolate-covered spaghetti...) $T$ units long, you can imagine taking successive nibbles without ever popping the entire remainder into your mouth. These bites constitute an infinite sequence of positive terms adding up to (no more than) $T$. (Of course, real confections in our universe are made of finitely many atoms, and cannot be divided into infinitely many pieces of positive size. You also have to imagine inhabiting a universe where continuum Pocky exists.)

More formally, consider the following procedure: If $T = T_{0} > 0$ is given, pick an arbitrary positive number $a_{1} < T_{0}$, and put $T_{1} = T_{0} - a_{1}$. Now repeat the process: If $n$ is a positive integer and $T_{n} > 0$ is given, pick an arbitrary positive number $a_{n+1} < T_{n}$, and put $T_{n+1} = T_{n} - a_{n+1}$.

This recursive procedure generates an infinite sequence $(a_{k})_{k=1}^{\infty}$ of positive numbers for which we have \begin{align*} \sum_{k=1}^{n} a_{k} &= a_{1} + a_{2} + \dots + a_{n} \\ &= \underbrace{(T_{0} - T_{1})}_{a_{1}} + \underbrace{(T_{1} - T_{2})}_{a_{2}} + \dots + \underbrace{(T_{n-1} - T_{n})}_{a_{n}} = T_{0} - T_{n} < T_{0}. \end{align*} That is, the "sum of all the terms" (strictly, the limit as $n \to \infty$ of the sum of the first $n$ terms) does not exceed $T_{0} = T$, and is equal to $T$ so long as the "leftovers" $T_{n}$ have no positive lower bound, e.g., you don't leave $31.415926\dots$ percent of the initial piece of licorice forever untouched "just in case you have guests someday".

Incidentally, there are many ways to "partition" a positive real number $T$ into infinitely many positive summands. Your friend Zeno of Elea might eat half of the remaining amount with each bite, or nine-tenths; your friend Salvadori Dali might vary the fraction with each bite. Each scheme of potential consumption gives you a sequence of positive real numbers adding up to a finite total.

Of course, all this leaves aside the generally difficult question: "If $(a_{k})_{k=1}^{\infty}$ is a sequence of (positive real) numbers, is the sum $\sum_{k} a_{k}$ finite or not?" But that's what convergence tests are for.