4

A tetrahedron $A-BCD$ is such all four faces are similar right triangle.

and we let $$AB=a,BC=b,AC=c,AD=d,BD=e,CD=f$$ define $$x=\max{(a,b,c,d,e,f)},y=\min{(a,b,c,d,e,f)}$$ show that: $$\dfrac{x}{y}=\sqrt{\dfrac{\sqrt{5}+1}{2}}$$

enter image description here

since $$\Delta Rt ABC\sim\Delta Rt ACD\sim\Delta Rt ABD\sim\Delta Rt BCD$$ Now we must suru which angle is right anlge,But I fell ugly,can you help me,and I think this is interesting problem.

it is said this problem have other solution $$\dfrac{x}{y}=\sqrt{2}?$$ this is true ? Thank you

Community
  • 1
math110
  • 93,304
  • "Regular" is usually used to indicate that all faces are equilateral and equivalent; by definition, a tetrahedron with right-triangular faces can't be regular. – Steven Stadnicki Apr 11 '14 at 05:53
  • Oh,Thank you @StevenStadnicki,I have edit. – math110 Apr 11 '14 at 06:11
  • 1
    Can't be a coincidence that the expression inside the surd is the golden ratio. – rah4927 Apr 11 '14 at 06:17
  • The $\sqrt{2}$ solution arises from the case of a "flat" tetrahedron: Take $ABCD$ to be a square with diagonals $AC$ and $BD$. – Blue Apr 11 '14 at 08:03
  • You can also take $ABCD$ to be a "flat" tetrahedron in the form of a rectangle. In that case, you can make two opposite sides of the rectangle as short as you like, and the other two opposite sides as long as you like (with the diagonals becoming even longer), so that $x/y$ has no upper bound. – Blue Apr 11 '14 at 11:07
  • @Blue,why? can you post you solution? Thank you – math110 Apr 11 '14 at 18:02
  • If $ABCD$ is a rectangle (a "flat" tetrahedron) with $AB = CD = 1$ and $AD = BC = k$ (where we may assume $k \geq 1$), then $x = \sqrt{1+k^2}$ and $y = 1$, so that $x/y = \sqrt{1+k^2}$. This value can be arbitrarily large, so the question "What is $x/y$?" has no specific answer; on the other hand, it can be no smaller than $\sqrt{2}$, so perhaps your question is actually "What is $\operatorname{min} x/y$?". (For the case of non-flat tetrahedra, the value might be $\sqrt{(\sqrt{5}+1)/2}$, but I haven't looked too hard, because of the vagueness of the question.) – Blue Apr 12 '14 at 01:03

1 Answers1

4

${\bf 1\ }$ Assume the side $BD=e$ (dashed in the figure) is a longest side of the tetrahedron. Then it has to be the hypotenuse of both adjacent triangles $ABD$ and $CBD$, so these two triangles have to be congruent.

${\bf 2\ } $ If $BA=BC$ then both triangles $BAC$ and $DAC$ are isosceles with hypotenuse $AC$. Claim: In this case the tetrahedron is flat, making up a square.

Proof. Assume the four points $A$, $B$, $C$, $D$ are not lying in a plane. Then there is exactly one sphere containing all four points. Therefore the two Thales spheres over $BD$ and $AC$ must coincide. It follows that $BD$ and $AC$ intersect in their midpoints, proving that our assumption is untenable.

${\bf 3\ }$ Therefore we may assume $a=BA=DC<BC=DA=b$, where $$a^2+b^2=e^2\ .\tag{1}$$ When triangle $BAC$ has its right angle at $B$ then necessarily $AC=e$, which enforces triangle $DAC$ to have its right angle at $D$, and it follows as in ${\bf 2\ }$ that the tetrahedron is flat, making up a rectangle.

${\bf 4\ }$ As $a<b$ it remains to consider the case that triangle $BAC$ has its right angle at $A$, and triangle $DAC$ has its right angle at $C$. $AC=c$ is then shortest side. It follows that $$b^2-a^2=c^2\ ,\tag{2}$$ and the similarity condition enforces $${a\over c}={b\over a}\ .\tag{3}$$

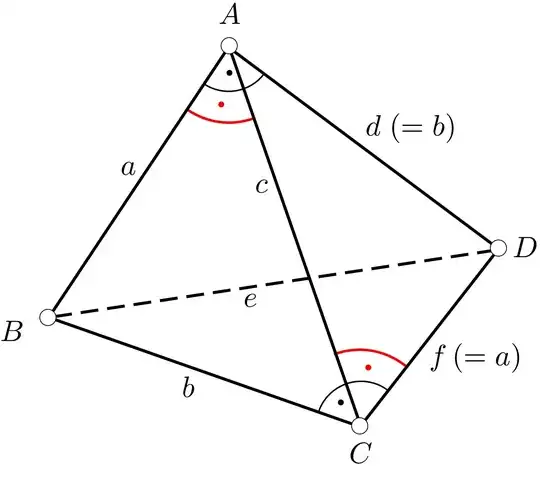
enter image description here

From $(1)-(3)$ we obtain after some computation $${e\over c}=\sqrt{2+\sqrt{5}}\ ,$$ which is almost what the OP claimed.

Christian Blatter
  • 226,825