I would like to do the following transformations on a very low resolution bitmap (64x64 pixels).
I am doing this transformation on a computer images, but it has nothing to do with computers, you can think about an image as rectangular grid with a real number mapped for each integer coordinate. I represent each point in a tuple (x, y, value). This means that my original image is just a set of points represented this way.
I will be doing geometric transformations on all the points.
- Moving the non-white areas to the center
- Scaling the non-white parts to fill the boundary
- Possibly doing some rotation and
- shearing.
My problem is that so far all the transformations are working perfectly, but I don't understand the theory behind that how can I put back a rotated, sheared, scaled, moved grid into the original 64x64 one.
I read articles about interpolating, and all of them starts by a point inside a 0..1, 0..1 unit square.
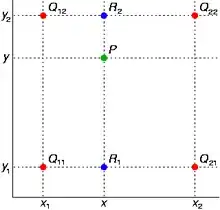
I understand this case (looks like a simple scaling), but in my case I don't know what is my reference grid and what are my pixels.
Can you explain to me that in a case where you do a series of transformations what is the reference grid, what are my points and that most importantly how do I get the transformed points back onto a 64x64 grid?