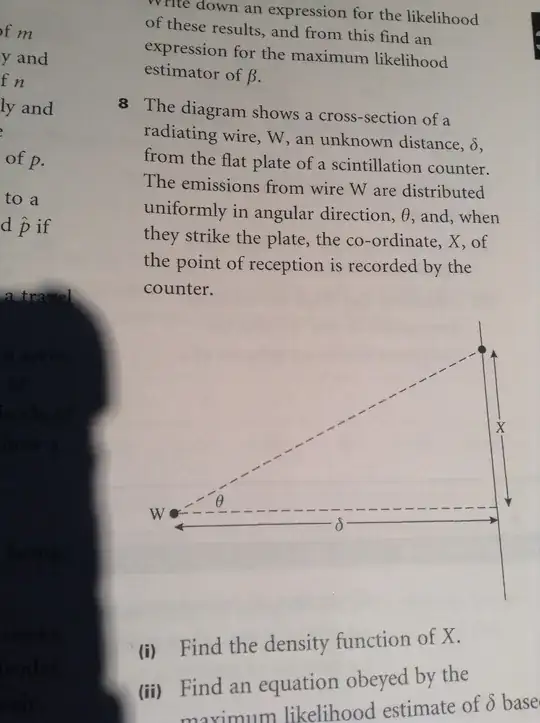
Please can someone expalin how i do question 8i in this picture, I have tried finding X in terms of theta but don't know then how to turn this into a pdf (if that is even what it is looking for)? I have basically got to x=δtan(θ)but don't know how to contiune?? Please help?