Why is the derivative of circle area the circumference?

Question

Why is the derivative of the volume of a sphere the surface area? And why is the derivative of the area of a circle the circumference? Too much of a coincidence, there has to be a reason! Also, why is the sum of the cubes the square of the sum of the integers?

Answer 1

Think about if you try to integrate the area of a circle by adding up the circumferences of all the smaller circles with radii from 0 to r (the radius of the big circle):

$\int_0^r 2\pi x \:\mathrm{d}x = \pi x^2|_0^r = \pi r^2$

So yes it is hardly a coincidence and is actually necessary that the area is the anti-derivative of the circumference.

As for the sum of cubes being equal to the square of the sum of integers, you can do it by induction:

Assume that

$1^3 + 2^3 + 3^3 ... n^3 = (1+2+3\:...\:n)^2$

You can then see that for n+1:

$1^3 + 2^3 + 3^3 ... (n+1)^3\\ = (1+2+3\:...\:n)^2 + (n+1)^3\\ = (n(n+1)/2)^2 + (n+1)^3$

which with a little bit of algebra can be shown to equal

$((n+1)(n+2)/2)^2\\ =(1+2+3\:...\:n+1)^2$

Answer 2

I'll answer the last question first because that's the easiest one in my opinion.

---

Prove that $$1^3 + 2^3 + 3^3 + \cdots + n^3 = \left(\frac{n(n+1)}{2}\right)^2$$

We will prove this using induction, by first confirming the identity when $n = 1$ and then proving the inductive step.

Base Case: $n = 1$

$$1^3 = \left(\frac{1(1+1)}{2}\right)^2 = \left(\frac{2}{2}\right)^2 = 1^2 = 1$$

Inductive Step:

Suppose the equality is true for some $x$. That is, $$1^3 + 2^3 + 3^3 + \cdots + x^3 = \left(\frac{x(x+1)}{2}\right)^2$$

Now we add $(x+1)^3$ to both sides and get

$$1^3 + 2^3 + 3^3 + \cdots + x^3 + (x+1)^3 = \left(\frac{x(x+1)}{2}\right)^2 + (x+1)^3 = (x+1)^2 \left(\frac{x^2}{4} + x + 1\right) = \frac{(x+1)^2}{4} (x^2 + 4x + 4) = \frac{(x+1)^2 (x+2)^2}{4} = \left(\frac{(x+1)(x+2)}{2}\right)^2$$

Therefore, if the equation is true for some $x$, then it is also true for $x+1$. And because it is true for $1$, it will be true for $2$, for $3$, for $4$, etc.

---

Prove that the derivative of the area of the circle is the circumference.

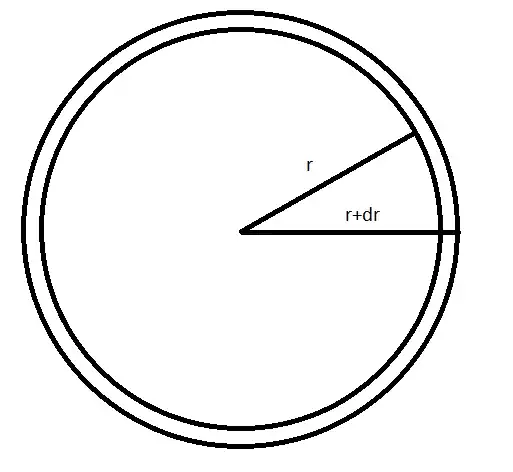
We note that the area of the bigger circle is $\pi (r+dr)^2$ and that of the smaller circle is $\pi r^2$. The difference in area, therefore, is $\pi (r+dr)^2 - \pi r^2 = \pi (2rdr + dr^2)$

We can then imagine turning the small "outline" (the area between the large circle and the small circle) into a thin, narrow strip. Assuming that $dr$ is small enough, the strip will be almost a rectangle with area $\pi (2rdr + dr^2)$. Because the height of the rectangle is $dr$, we divide the area by the height to get the width, which is $$\frac{\pi (2rdr + dr^2)}{dr} = \pi (2r + dr)$$

And finally, because $dr$ approaches $0$ as the strip gets thinner, we see that the width approaches $2\pi r$, the circumference.

Similar logic applies to the sphere and the surface area.

Answer 3

For the first two questions, picture a circle of radius $r$ and a circle of radius $r+Δr$. The question is how much bigger is the second circle (in terms of area). The second circle is $\pi(r+\Delta r)^2-\pi r^2=\pi (2r\Delta r +(\Delta r)^2$. Dividing by $\Delta r$ and taking the limit as $\Delta r\to 0$ yields $2\pi r$.

Informally, if you want to increase the area by a sliver, you would add another small layer just outside the perimeter of the circle.

The sphere problem is the same.

Answer 4

Well, we will interpret the statement "derivative of the volume of a sphere is surface area" as "integral of surface area is volume". This statement should be trivial. Assuming the initial surface area (i.e., the surface area at any point on the sphere's surface) is $0$, we know that the infintesimal volume element is simply: $$dV=S(A)dR\\\text{ (Can you see why? Hint: Use polar coordinates, or, if you're feeling geometric, }\\\text{ the fundamental theorem of calculus.)}$$ Thus, we may generalize to arbitrary dimensions (remaining in Euclidean space, of course) $$dV_{n\text{ dimensions}}=V_{(n-1)\text{ dimensions}}dR$$ In fact, there's a whole paper on it!