My textbook says:
$$\overline{s}_n = \sup \{a_n \mid n \geq N\}$$
and $\operatorname{limsup} \{a_n\}_{n \to \infty} = \lim_{N \to \infty} \overline{s}_N$.
Also, it says: As $N$ gets larger, the sup is taken over a smaller set, so the sequence of numbers $\{\overline{s}_n\}$ is monotone decreasing.
I don't understand why this must be the case. If we have a sequence $3-1/n$, then as $n$ gets larger, don't the sequence values (and hence the supremums in each interval) get larger?
I know you already accepted an answer, but nothing does it like a picture for me. Imagine our sequence does something like this where $n$ increases in the positive $x$ direction.
Then the limsup of this sequence would be the redline (not the axis).
But if the sequence looks like this,
our limsup will do this.
When I first learned about $\limsup$ and $\liminf$ I found it helpful to think of them as, respectively, "eventual least upper bound" and "eventual greatest lower bound". They are variants of the LUB and GLB that avoid taking account of any finite number of (possibly "deviant") terms of the sequence, but only record the limiting trend in how high or how low the terms get.
If you take any set $S$ of real numbers and remove some values to get a smaller set $S' \subset S$, then $\sup S' \leq \sup S$ by definition (any upper bound of $S$ is an upper bound of $S'$, in particular the LUB of $S$). The key point, which I think you are missing, is that in the definition of $\limsup a_n$, the $s_N$ are defined to be over all $n \geq N$, so for an increasing sequence like the one you gave, all the $s_N$ are equal (in this case to $3$).
It means "weakly" decreasing, so they may not get smaller, but they don't get larger. Let's look at $3-1/n$. \begin{align} & \sup\left\{3 - \frac1 1, 3-\frac12,3-\frac13,3-\frac14,3-\frac15,\ldots\right\} \\[8pt] & \sup\left\{ 3-\frac12,3-\frac13,3-\frac14,3-\frac15,\ldots\right\} \\[8pt] & \sup\left\{3-\frac13,3-\frac14,3-\frac15,\ldots\right\} \\[8pt] & \sup\left\{3-\frac14,3-\frac15,\ldots\right\} \\[8pt] & {}\qquad \vdots \end{align}
The sequence of suprema gets (weakly) smaller.
The sequence values increase but the suprema over the tails decrease because the supremum is taken over smaller and smaller sets.
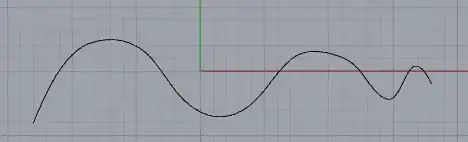
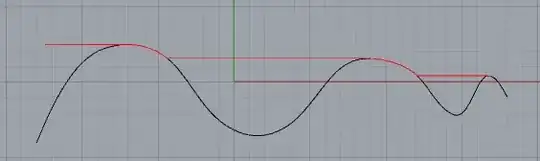
This analogy may help: Imagine a piston at $+\infty$ moving leftward until it stopped by the presence of the sequence $a_1,a_2\ldots$. The place will stop is the $\sup$ of the sequence, which in your notation is $\overline s_1$, i.e., the first element of the sequence $(\overline s_n)$. Now let remove the first element $a_1$ of the original sequence, this may or may not change the $\sup$ of the sequence. If will change the $\sup$, the piston slip leftward to a new point $\overline s_2$. If not, then the piston will not move and $\overline s_2$ will be the same as $\overline s_1$. In any case $\overline s_2$ cannot be greater than $\overline s_1$. Then we remove the second element $a_2$, causing the piston to slip a little more. If we keep doing this the piston will keep slipping, but there will be a point where cannot go any further and this is what we call the limit superior of the sequence.
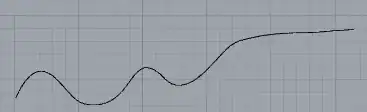
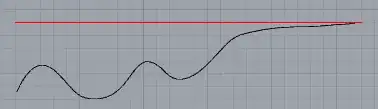
Now more formally the sequence $(\overline s_n)$ is non-increasing, i.e., is monotone, so the limit of the sequence always exists in the extended real numbers, and this limit, which is the infimum, is what we call the limit superior.
