Area covered by a constant length segment rotating around the center of a square.

Question

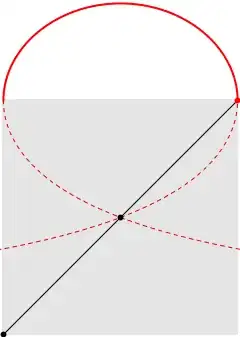
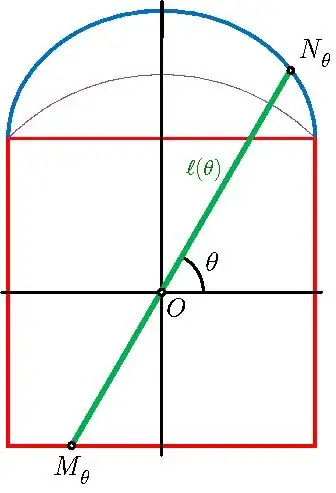
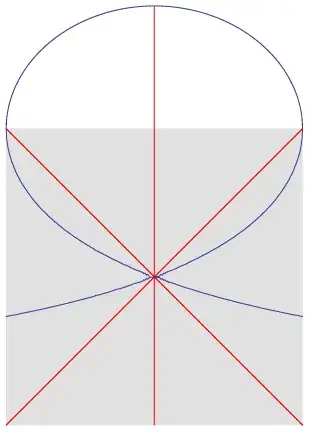
This is an idea I have had in my head for years and years and I would like to know the answer, and also I would like to know if it's somehow relevant to anything or useless. I describe my thoughts with the following image:

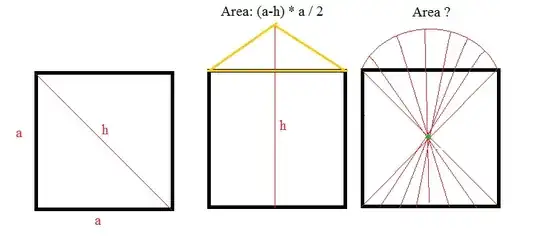
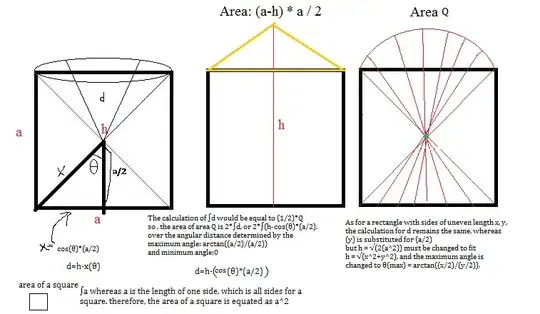
What would the area of the "red almost half circle" on top of the third square be, assuming you rotate the hypotenuse of a square around it's center limiting its movement so it cannot pass through the bottom of the square.
My guess would be:

$$\ \frac{\left(\pi*(h/2)^2 - a^2\right)}{2}$$

And also, does this have any meaning? Have I been wandering around thinking about complete nonsense for so many years?

Answer 1

I found this problem interesting enough to make a little animation along the line of @Blue's diagram (but I didn't want to edit their answer without permission):

Mathematica syntax for those who are interested:

G[d_, t_] := {t - (d t)/Sqrt[1 + t^2], d /Sqrt[1 + t^2]}
P[c_, m_] := Show[ParametricPlot[G[# Sqrt[8], t], {t, -4, 4}, 
 PlotStyle -> {Dashed, Hue[#]}, PlotRange -> {{-1.025, 1.025}, {-.025, 
               2 Sqrt[2] + 0.025}}] & /@ (Range[m]/m), 
 ParametricPlot[G[Sqrt[8], t], {t, -1, 1}, PlotStyle -> {Red, Thick}], 
 Graphics[{Black, Disk[{0, 1}, .025], Opacity[0.1], Rectangle[{-1, 0}, {1, 2}],
           Opacity[1], Line[{{c, 0}, G[Sqrt[8], c]}], Disk[{c, 0}, .025],
           {Hue[#], Disk[G[# Sqrt[8], c], .025]} & /@ (Range[m]/m)}],
 Axes -> False]
Manipulate[P[c, m], {c, -1, 1}, {m, 1, 20, 1}]

Answer 2

Let $O$ be the center of the square, and let $\ell(\theta)$ be the line through $O$ that makes an angle $\theta$ with the horizontal line. The line $\ell(\theta)$ intersects with the lower side of the square at a point $M_\theta$, with $OM_\theta=\dfrac{a}{2\sin \theta }$. So, if $N_\theta$ is the other end of our 'rotating' diagonal then we have $$ON_\theta=\rho(\theta)=h-OM_\theta=a\sqrt{2}-\dfrac{a}{2\sin \theta }.$$ Now, the area traced by $ON_\theta$ as $\theta$ varies between $\pi/4$ and $3\pi/4$ is our desired area augmented by the area of the quarter of the square. So, the desired area is $$\eqalign{ \mathcal{A}&=\frac{1}{2}\int_{\pi/4}^{3\pi/4}\rho^2(\theta)\,d\theta-\frac{a^2}{4}\cr &=a^2\int_{\pi/4}^{\pi/2}\left(\sqrt{2}-\frac{1}{2\sin\theta}\right)^2\,d\theta-\frac{a^2}{4} &=a^2\left(\frac{\pi}{2}-\sqrt{2}\ln(1+\sqrt{2})\right) } $$ Therefore, the correct answer is about $13.6\%$ larger than the conjectured answer.

Answer 3

To avoid some fractions, I'll define $b := a/2$, so that the side of the square is $2b$ and its diagonal has length $2b\sqrt{2}$. Position the square so that its bottom lies on the $x$-axis, and its center lies on the $y$ axis (specifically, at $(0,b)$).

A tilted diagonal determines a line through $(0,b)$ and, say, $(c,0)$, with $c$ some parameter such that $-b \leq c \leq b$. Such a line has equation $$\frac{x}{c} + \frac{y}{b} = 1 \qquad \to \qquad x b + y c = b c \qquad (\star)$$ The upper endpoint, $(x,y)$, of the tilted diagonal is a distance $2b\sqrt{2}$ from $(c,0)$: $$(x-c)^2 + y^2 = 8 b^2 \qquad (\star\star)$$ Eliminating $c$ from $(\star)$ and $(\star\star)$ gives $$x^2 = \frac{(y-b)^2 (8 b^2 - y^2)}{y^2}$$ This equation represents this graph:

The area of the portion above the square can be determined via this integral:

$$2\;\int_{2b}^{2b\sqrt{2}}\frac{y-b}{y}\sqrt{8b^2-y^2} \; dy = 2b^2 \left( \pi - 2 \sqrt{2} \log( 1 + \sqrt{2} ) \right) = a^2 \left( \frac{\pi}{2} - \sqrt{2} \log(1+\sqrt{2})\right)$$ which agrees with both @OmranKouba and @IanMateus.

Answer 4

This isn't really an answer, but I wanted to record my observation that the curve in question is not actually a circle.

Let's say the square has corners at $(\pm 1, \pm 1)$ so that the center is at the origin (and the diagonal has length $\sqrt{8}$). If we fix a point $(s,-1)$ on the lower edge of the square, the line through $(s,-1)$ and $(0,0)$ is parametrized by $t \mapsto (-ts, t)$. The point on this line which is distance $\sqrt{8}$ from $(s,-1)$ corresponds to $t$ being the positive solution of $$(-ts-s)^2+(t+1)^2=8$$ which is $$t = -1 + \sqrt{\frac{8}{s^2+1}}.$$ So the curve is parametrized by $$(x(s),y(s)) = \left( s - s\sqrt{\frac{8}{s^2+1}}, -1+\sqrt{\frac{8}{s^2+1}}\right).$$ If this is indeed a circle, by symmetry its center must be on the $y$-axis at some point $(0, y_0)$ in which case we must have $$x(s)^2 + (y(s)-y_0)^2 = \text{const}$$ or, differentiating, $$2 x(s) x'(s) + 2 (y(s)-y_0) y'(s) = 0.$$ Solving, we find that we must have $$y_0 = \frac{x(s) x'(s)}{y'(s)} + y(s).$$ But this is not constant. When $s=0$ the right side is $\frac{4-\sqrt{2}}{4}$ while if $s=1$ we get $1$.

Answer 5

I'm not like super expert at math, and I only kind of checked my work, but I'm pretty sure this crudely-drawn msPaint picture is correct.

Answer 6

(Misinterpreted question, working on the correct version), the second part still holds.

The other question:

Does this have any meaning? Have I been wandering around thinking about complete nonsense for so many years?

I am not sure what you mean, to me all math is meaningful. There is no such thing as meaningless in math, unless you write something obviously absurd like

$$\frac{1}{8}- \text{tomato} = ??$$

Now, yours is certainly a valid question, with some applications in engineering, I presume. Sure the above calculation isn't ground breaking -- fairly elementary in fact -- but it could come up.

Also, I do see some hints and traces of the Isoperimetric problem which discusses how efficient a shape is at enclosing an area, and circles happen to be the most efficient, a property that translates into volume-area efficiency in spheres -- which is the reason behind why all major celestial bodies are (almost) spheres, why bubbles are spherical, why raindrops are spherical, et cetera.