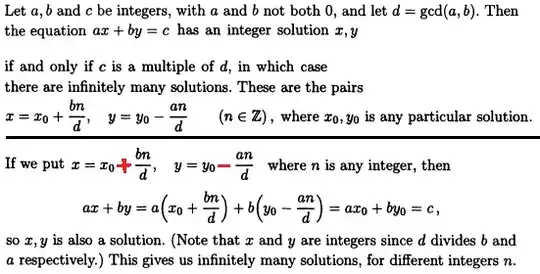(1) Can't the signs - I colored them in red - of x and y be switched? Aren't $x = x_0 - bn/d$ and $y = y_0 + an/d$ also solutions? They satisfy $ax + by = c$?
(2) How can I remember these general solutions? Where did $x,y$ hail from? Jones didn't delineate how he found them?
Origin - Elementary Number Theory, Jones,
p10, Theorem 1.8.
The sentence starting with 'These are the pairs' is p13, Theorem 1.13
Let's ask ourselves the question that Jones would have asked himself.
$ax + by = c\tag{1}$
Assume we can, and let $\begin{align}x' = x_0 + s\\y' = y_0 + t\end{align}\tag{2}$
where $s, t \in \mathbb{Z}$ are the differences between $x', x_0$ and $y', y_0$ respectively.
Since $x', y'$ satisfy $(1)$ $\begin{eqnarray} & ax' + by' &= c\\\implies &a(x_0 + s) + b(y_0 + t) &= c\\\implies &ax_0 + by_0 + as + bt &= c\\\implies & c + as + bt &= c\\\implies &as + bt &= 0\\\implies&\frac{s}{t} &= -\frac{b}{a} \\\implies&\frac{s'}{t'}&= -\frac{b'}{a'} \text{ (lowest form)}\tag{3}\end{eqnarray}$
where $b' = \frac{b}{\gcd{(a, b)}}$ and $a' = \frac{a}{\gcd{(a, b)}}$. Similarly for $s'$ and $t'$.
$(3)\implies \begin{matrix}s' &= &-b' &\implies &s = s'\gcd(s, t) &= &-b'\gcd(s, t)\\t' &= &a' &\implies &t = t'\gcd(s, t) &= &a'\gcd(s, t)\end{matrix}$
Substituting in $(2)$,
$\begin{matrix}x' = x_0 + s = x_0 -b'\gcd(s, t) = x_0 - (b/d)n\\y' = y_0 + t = y_0 + a'\gcd(s, t) = y_0 + (a/d)n\end{matrix}\tag{4}$
where $d = \gcd(a,b)$ and $n = \gcd(s, t)$.
Since $n$ gets cancelled out from both numerator and denominator of $\frac{s}{t}$ to give $\frac{s'}{t'} $, it is free to have any integer value.
We can thus generate an infinite number of solutions $x'$ and $y'$ to $(1)$, each determined by a different $n \in \mathbb{Z}$ substituted in $(4)$.
