Why if $a = qb + r$, then $\operatorname{gcd}(a,b) = \operatorname{gcd}(b, r)$ intuitively?

Question

Origin - Elementary Number Theory, Jones, p $5$, Lemma $1.5$

Are there any illustrations? I tried Wikipedia's article and the first picture to the right, but I think this delineates Euclid's Algorithm? I'm not querying about proofs.

Answer 1

This is how I visualized it:

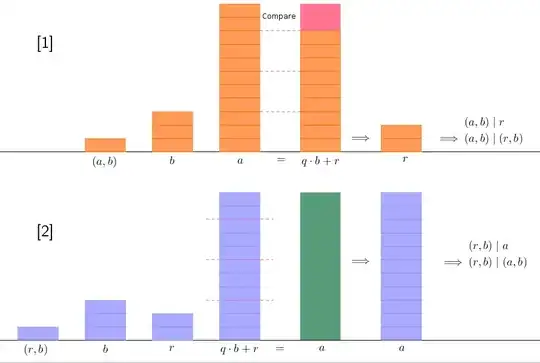
where $(x, y)$ denotes $\text{gcd}(x, y)$.

Explanation:

Arithmetic of blocks:

An integer $x$ is represented by a rectangular block of unit width and height $x$. Arithmetic operations between integers can then be visualized as manipulation of their blocks.

• $x + y$: Put a block of height $y$ on top of a block of height $x$ to produce a new block of height $x + y$.
• $x - y$: Remove a block of height $y$ from a block of height $x$ to produce a new block of height $x - y$.
• $x \cdot y$: Put $y$ blocks of height $x$ on top of each other to produce a new block of height $x \cdot y$.

Main idea in the diagram:

Use blocks of height $(x, y)$ to argue about divisibility.

Representation:

By definition, $x = (x, y) \cdot k_1 \text{ and } y = (x, y) \cdot k_2 \text{ where } k_1, k_2$ are integers. So, $x$ and $y$ can be drawn as a stack of some integral number of blocks each of height $(x, y)$.

Part 1:

• Put $x = a, y = b$ to get the first three towers. I chose $k_1 =11$ and $k_2 = 3$ just as an example (to keep my drawing task manageable :)
• The fourth tower represents $q \cdot b + r$.
• $a = q \cdot b + r$ tells us that the third and fourth towers are identical. So, we get by visual inspection that $r = a - q \cdot b$ is the fifth tower.
• Thus, $r$ is shown to be made up of the "building block" $(a, b)$. That is, $r = (a, b) \cdot k_3$ for some integer $k_3$. I chose $k_3 = 2$ just as an example.
• We observe that $(a, b)$ divides both $r$ and $b$, and so it must divide $(r, b)$.

Part 2:

• Put $x = r, y = b$ to get the first three towers. I could have chosen different $k_i$'s than in Part 1, but since they eventually turn out to be the same, I didn't do it.
• The fourth tower represents $q \cdot b + r$.
• The fifth tower represents $a$.
• $a = q \cdot b + r$ tells us that the fourth and fifth towers are identical. So, by visual inspection we get that $a$ is the sixth tower, composed of the "building block" $(r, b)$. That is, $a = (r, b) \cdot k_4$ for some integer $k_4$. I chose $k_4 = 11$ to match with Part 1.
• We observe that $(r, b)$ divides both $a$ and $b$, and so it must divide $(a, b)$

Implication:

I leave it for the reader to conclude that $x | y \text{ and } y | x \implies x = y$. That is, $(a, b) = (r, b) \blacksquare$

Note:

I chose positive integers in the diagram, but one could imagine negative integers as blocks below the horizontal line, representing negative height. But this would clutter the illustration.