Is it true that for any $0<c<1/2$ and sufficiently large $n'$, there exists a $d <2$ such that ${n \choose cn} < d^n$ for all $n>n'$? Clearly we have to assume $cn$ is an integer.
I saw Bounds for $\binom{n}{cn}$ with $0 < c < 1$. but I couldn't see how to use that here.
Hint: Use the Stirling formula.
When you do so, it remains $$ \binom n{cn}\sim \frac{1}{\sqrt{c(1-c)n}c^{cn}(1-c)^{(1-c)n}} =\frac{1}{\sqrt{c(1-c)n}} \left(c^{-c}(1-c)^{c-1}\right)^n $$ For $n$ large enough and $d> (1-c)^{c-1}c^{-c}$, you have $$ \binom n{cn}< d^n $$
Now as $c<1/2$,
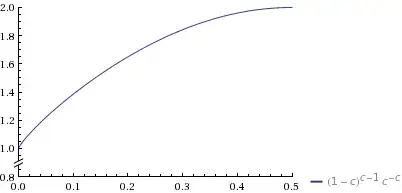
you can take $d$ such as $$ (1-c)^{c-1}c^{-c}<d<2 $$
A direct proof of the last inequality is also possible: using the AM-GM inequality,
$$ (1-c)^{c-1}c^{-c} =\left[\frac 1{1-c}\right]^{1-c} \left[\frac 1{c}\right]^{c}< \frac 1{1-c}{1-c} + \frac 1cc=2 $$ with a strict inequality because $c\neq \frac 12 \implies 1-c\neq c$
