1

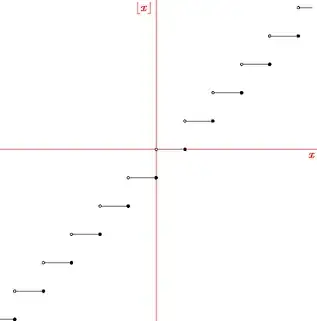
I'm reading Calculus: Basic Concepts for High School Students and am trying to digest the definition of 'limit of function'. There are two details that I am struggling to fully accept:

  1. If you are supposed to pick an interval $(a - \delta, a + \delta)$ but $a$ can be an undefined point at the end of the domain, what happens to the other half of the interval? Is it just ignored/irrelevant?

  2. The function used as an example is $f(x) = \sqrt{x}$ and from what I can tell the limit of the point $a$ always matches the value of $f(a)$. I cannot see how this would be different for other functions given the way that the limit is calculated - if someone could share an example of a function that has a different limit at $x = a$ than the value $f(a)$ I would be grateful.

Git Gud
  • 31,356
Matt Martineau
  • 151
  • I'm guessing you, at least informally, are aware of the concept of discontinuous function. Discontinuous functions are examples for 2. – Git Gud Apr 03 '14 at 09:02
  • Thank you, I had spent a short time looking at continuity and now understand it's relation to limits of functions. $\lim \limits_{x \to a} f(x) = f(a)$ actually means the function is continuous at point $a$. – Matt Martineau Apr 03 '14 at 12:46
  • http://math.stackexchange.com/questions/1156419/precise-definition-of-limit/1540328#1540328 –  Nov 22 '15 at 11:25

3 Answers3

2

  1. Yes, if your function is defined on $[a,b]$ and you want to compute the limit in $b$, you can only consider what is happening in $[b-\delta, b]$

  2. Look at the function floor(x) which is defined as the highest integer that is less than equal to x. Here is the graph :

enter image description here

The limit on 1 does not properly exist. There is a right-sided limit which is 1 and the value of f in 1. However the left-sided limit in 1 is 0 and is not the value of f in 1.

T_O
  • 629
1

Any function that has a jump discontinuity is an example. Take for example the function defined by: $f(x) = x$ if $x\ne 4$, $f(x) = 5$ if $x=4$. Then $$\lim_{x\to 4}f(x) = 4$$ but $f(4) = 5$.

Rustyn
  • 8,407
1
  1. Consider $f(x)=\sqrt{x}$. It is naturally defined on the set $[0,+\infty)$, and it would be wrong to consider subsets like $(-1,1)$, since such an interval is not a subset of the domain of definition.
  2. What you are saying could be translated into the sentence that "every function is a continuous function". This is clearly false, as you can read in every calculus book. For example, $\lim_{x \to 0} \frac{1}{x^2}=+\infty$, and you can't define the function $f(x)=\frac{1}{x^2}$ at $x=0$ so that $f(0)=+\infty$.
Siminore
  • 35,136