Prove $\sin^2 A = \sin^2 B \sin^2 C - 2\sin B \sin C \cos A$

Question

I am asking for help with this proof:

Given $\triangle ABC$. Prove that $\sin^2 A = \sin^2 B+ \sin^2 C - 2\sin B \sin C \cos A$

Answer 1

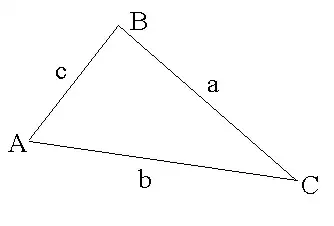
Let us write the Al Kashi formula: $$a^2 = b^2 + c^2 -2bc\cos A $$ and the sine law:$$ \frac{\sin A}a = \frac{\sin B}b = \frac{\sin C}c $$hence:

$$ \sin^2 A = a^2\frac{\sin^2 A}{a^2} = (b^2 + c^2-2bc\cos A)\frac{\sin^2 A}{a^2}\\ = b^2\frac {\sin^2 B}{b^2}+c^2\frac {\sin^2 C}{c^2} - 2 bc \cos A\frac{\sin B}b \frac{\sin C}c \\ \sin^2 A= \sin^2 B+\sin^2 C -2\sin B\sin C \cos A $$

Answer 2

Using Prove that $\sin^2(A) - \sin^2(B) = \sin(A + B)\sin(A -B)$ and $\displaystyle A+B+C=\pi\iff A+B=\pi-C,\sin(A+B)=\sin(\pi-C)=\sin C$

$$\sin^2A-\sin^2B-\sin^2C$$ $$=\sin(A+B)\sin(A-B)-\sin C\sin C$$ $$=\sin(\pi-C)\sin(A-B)-\sin C\sin\{\pi-(A+B)\}$$ $$=\sin C\sin(A-B)-\sin C\sin(A+B)$$ $$=-\sin C[\sin(A+B)-\sin(A-B)]$$ $$=-\sin C[2\sin B\cos A]$$