4

Looking through the webcomic, I came across one of my favorite comics:

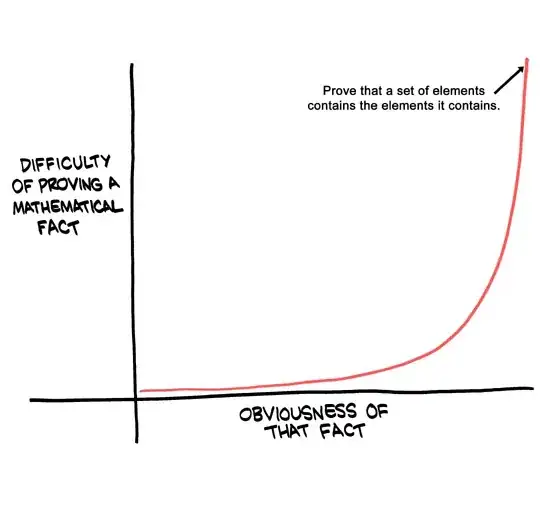
enter image description here

(from Saturday Morning Breakfast Cereal)

It seems that people have an ongoing interest in results in mathematics that are true, but highly unintuitive, like the Banach-Tarski Paradox. However, what results are there that are seemingly obvious and intuitive, but difficult to prove (or perhaps have non-obvious intricacies)?

I feel that such examples are important for helping people understand the necessity of rigor or that seemingly obvious results are not at all obvious from a mathematical perspective.

(Personally, I don't feel that 'simple' number theory conjectures/results like the ABC conjecture fall under this category, because while simple to state, they are often very removed from reality.)

Hayden
  • 16,737
  • I don't know that I'd call the ABC conjecture simple to state (at least compared to, say, FLT.) –  Mar 29 '14 at 01:31
  • 1
    Relating to the statement in the comic more than your question: Obvious facts are generally easier to prove. However, when one is first learning mathematics, one generally does not develop the necessary machinery to prove anything from axioms, so proofs are done by reducing complex statements to the more obvious ones. In the case of already obvious statements there is no point to this, so the necessary machinery must be developed and used for there to be anything to do. However, this is still easier than proving more complex statements from equally basic principles. – Alex Becker Mar 29 '14 at 01:33
  • Agreed, but I wanted to reference an open question, though there are obviously other simpler to state open questions out there. – Hayden Mar 29 '14 at 01:33

3 Answers3

10

The Jordan curve theorem asserts that every a non-self-intersecting continuous loop divides the plane into an "interior" region bounded by the curve and an "exterior" region.

Another nice example is the P vs NP problem, which basically says verifying is easier than finding solutions. But it is still unsolved , one of the Clay Millennium problems.

Mohan
  • 14,856
1

Prove the reflexive property, or that $x = x$.

http://www.tondering.dk/claus/sur16.pdf

Crazy stuff.

louie mcconnell
  • 2,126
  • This is misleading, because if you're asking for a formal proof you need to give a formal statement; and a formal statement of "$x=x$ where $x$ is a surreal number" is definitely not simple, – Alex Becker Mar 29 '14 at 01:35
  • Yes. A more obvious fact, according to the expert graph, has a more difficult proof. – louie mcconnell Mar 29 '14 at 01:35
  • I'm not sure what your comment means. Can you clarify? – Alex Becker Mar 29 '14 at 02:14
  • The xkcd comic is implying that a very simple axiom can be very difficult to prove. This is one of the simplest axioms imaginable, with an extremely difficult proof. – louie mcconnell Mar 29 '14 at 02:40
0
  • $\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R} (x + y) + z = x + (y + z)$
  • $\forall x \in \mathbb{R}\forall y \in \mathbb{R}x + y = y + x$
  • $\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R} (x \times y) \times z = x \times (y \times z)$
  • $\forall x \in \mathbb{R}\forall y \in \mathbb{R}x \times y = y \times x$
  • $\forall x \in \mathbb{R}\forall y \in \mathbb{R}\forall z \in \mathbb{R} x \times (y + z) = (x \times y) + (x \times z)$
Timothy
  • 793
  • Proof of line 1, Proof of line 2, Proof of line 3, Proof of line 4, Proof of line 5. – Jam Jan 21 '20 at 20:23
  • Whether or not this is 'difficult' is entirely dependent on what we take as given. – Jam Jan 21 '20 at 20:24
  • @Jam The construction from Cauchy sequences is one possible definition. I don't actually like that definition much because some computable Cauchy sequences approach an uncomputable number. The construction from Dedekind cuts of the rational numbers is another definition and the proof in ZF using that definition is probably pretty complicated. I think that also the problem of computing whether two algorithms that generate a Cauchy sequence generate one that approaches the same number is uncomputable. – Timothy Jan 22 '20 at 01:06