3

The number of different solutions $(x,y,z)$ of the equation $x+y+z=10$ where each of $x, y$ and $z$ is a positive integer is $36$.

How to derive this answer?

I know that $x, y$ and $z$ have to be $1\leq x,y,z\leq8$ and $x,y,z\in\mathbb Z.$ This said me $8+7+6+5+4+3+2+1=36.$

But I can't understand the process of counting the solutions.

Martin Sleziak
  • 53,687
Silent
  • 6,520
  • 3
    For greater generality, please see the Wikipedia article on Stars and Bars. There you will see why the number is $\binom{10-1}{3-1}$. – André Nicolas Mar 25 '14 at 06:50
  • @AndréNicolas, THANK YOU SO MUCH, SIR! – Silent Mar 25 '14 at 07:01
  • 1
    You are welcome. The idea of making a list, and counting the number of solutions with $x=9$, the number of solutions with $x=8$, and so on, and adding up, works nicely for $x+y+z=n$. However, that sort of approach is not really feasible for $a+b+c+d+e+f=200$. But Stars and Bars gives immediate answer $\binom{200-1}{6-1}$. – André Nicolas Mar 25 '14 at 07:05

3 Answers3

2

Case 1: $x = 1$, $z = 9 - y$, $1 \le y \le 8$. That's the $8$.

Case 2: $x = 2$, $z = 8 - y$, $1 \le y \le 7$. That's the $7$.

etc,

Robert Israel
  • 448,999
2

Let $x = k + 1$, $y = m + 1$, and $z = n + 1$. Then you solve the equation: $k + m + n = 7$, and count the number of non-negative integers solution to this equation. It is a well known answer that it is: $\binom 9 2 = 36$.

Silent
  • 6,520
DeepSea
  • 77,651
1

A way of picturing this (illustrating what Robert Isreal describes) is to consider the tilted plane $ \ x + y + z = 10 \ . $ In the graph below, the lines of intersection with the coordinate planes are marked in red.

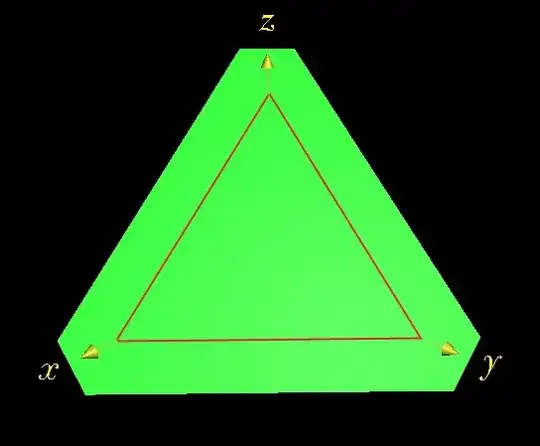
enter image description here

The number of positive integer solutions to the equation is the number of integer lattice points that lie on that plane and within the triangle indicated (since we are not to include zeroes in the sums). On the level $ \ z = 1 \ , $ there would then be eight such lattice points, seven on level $ \ z = 2 \ , $ and so on down to one on level $ \ z = 8 \ . $ This gives the number of permitted solutions as the eighth "triangular number", given as

$$ \left( \begin{array}{c} 8 + 1 \\ 2 \end{array} \right) \ = \ \frac{9!}{2! \ 7!} \ = \ 36 \ \ .$$

One could generalize this to say that the number of positive integer solutions to $ \ x + y + z \ = \ N \ $ (with integer $ \ N \ge 3 \ $ ) is the $ \ (N-2) th \ $ triangular number, $ \left( \begin{array}{c} N - 1 \\ 2 \end{array} \right) \ . $

colormegone
  • 10,842
  • Thank you for this amazing answer! – Silent Mar 25 '14 at 08:28
  • 1
    This is connected to the material discussed in the link André Nicolas gives in his comment above (which I saw only after I'd already posted). That "partitioning" argument is related then to the extension into higher dimensions: the number of positive integer solutions to $ \ x + y + z + w = N \ $ (for integer $ \ N \ge 4 \ $ ) is the $ \ (N-3) th \ $ "tetrahedral number", $ \left( \begin{array}{c} N - 1 \ 3 \end{array} \right) \ , $ and so on. – colormegone Mar 25 '14 at 14:36