3

Express the curve $r = \dfrac{9}{4+\sin \theta}$ in rectangular form. And what is the rectangular form?

If I get the expression in rectangular form, how am I able to convert it back to polar coordinate?

F.A.
  • 1,001
Victor
  • 8,372
  • Clear the denominator, distribute, and notice that $y=r\sin(\theta)$ and $r=\sqrt{x^2+y^2}$. – Bill Cook Oct 12 '11 at 21:00
  • 2
    "Rectangular form" means that instead of polar coordinates with $\theta$ an angle and $r$ the distance to the center, you must describe the points of the curve in a standard Cartesian ($x$, $y$) coordinate system. – hmakholm left over Monica Oct 12 '11 at 21:01
  • As @Bill mentioned, use $\sin\theta=\frac{y}{r}=\frac{y}{\sqrt{x^2+y^2}}$ and simplify. To get back the polar, undo (reverse) the process e.g., change $x=r\cos\theta$ and $y=r\sin\theta$. – Tapu Oct 12 '11 at 21:15

2 Answers2

6

what is the rectangular form?

It is the $y=f(x)$ expression of the curve in the $x,y$ referential (see picture). It can also be the implicit form $F(x,y)=F(x,f(x))\equiv 0$.

Steps:

1) transformation of polar into rectangular coordinates (also known as Cartesian coordinates) (see picture)

$$x=r\cos \theta ,$$

$$y=r\sin \theta ;$$

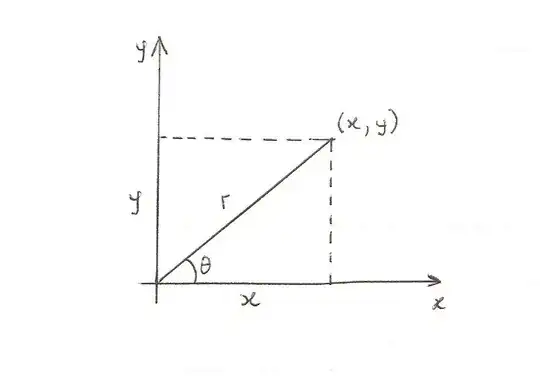
enter image description here

2) from trigonometry and from 1) $r=\sqrt{x^2+y^2}$

$$\sin \theta =\frac{y}{r}=\frac{y}{\sqrt{ x^{2}+y^{2}}};$$

3) substitution in the given equation $$r=\frac{9}{4+\sin \theta }=\dfrac{9}{4+\dfrac{y}{\sqrt{x^{2}+y^{2}}}}=9\dfrac{\sqrt{x^{2}+y^{2}}}{4\sqrt{x^{2}+y^{2}}+y};$$

4) from 1) $r=\sqrt{x^2+y^2}$, equate

$$9\frac{\sqrt{x^{2}+y^{2}}}{4\sqrt{ x^{2}+y^{2}}+y}=\sqrt{x^{2}+y^{2}};$$

5) simplify to obtain the implicit equation

$$4\sqrt{x^{2}+y^{2}}+y-9=0;$$

6) Rewrite it as $$4\sqrt{x^{2}+y^{2}}=9-y,$$ square it (which may introduce extraneous solutions, also in this question), rearrange as

$$16y^{2}+18y+15x^{2}-81=0,$$

and solve for $y$

$$y=-\frac{3}{5}\pm \frac{4}{15}\sqrt{81-15x^{2}}.$$

7) Check for extraneous solutions.

if I get the expression in rectangular form, how am I able to convert it back to polar coordinate?

The transformation of rectangular to polar coordinates is

$$r=\sqrt{x^{2}+y^{2}}, \qquad \theta =\arctan \frac{y}{x}\qquad \text{in the first quadrant},$$

or rather $\theta =\arctan2(y,x)$ to take into account a location different from the first quadrant. (Wikipedia link).

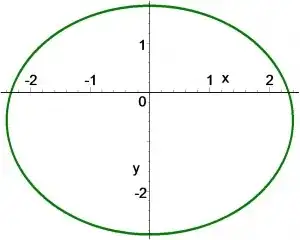
As commented by J.M. the curve is an ellipse. Here is the plot I got using the equation $16y^{2}+18y+15x^{2}-81=0$.

enter image description here

Community
  • 1
Américo Tavares
  • 38,602
  • As a check: the original polar equation is in fact that of a conic with focus at the origin. Rewriting the expression as $r=\dfrac{\frac94}{1+\frac14\sin,\theta}$, we find that we have an ellipse with eccentricity $\frac14$. The same result can be seen if we use completing the square to convert the Cartesian equation to a standard form and compute the eccentricity from the values of the semimajor and smiminor axes... – J. M. ain't a mathematician Oct 13 '11 at 11:09
  • @J.M. Thanks! I added a picture. – Américo Tavares Oct 13 '11 at 11:29
2

$$ 4r + 4r\sin\theta = 9. $$ Therefore $$ \sqrt{x^2+y^2} + 4y = 9. $$ $$ \sqrt{x^2+y^2} = 9 - y. $$ Now square both sides and go on from there.

But remember that squaring both sides can lead to extraneous roots. For example $3^2=9$ and $(-3)^2=9$, so a "$\pm$" is introduced when you go back to the unsquared form. In other words, the graph you get after squaring may contain additional points beyond those you should get, and you have to check for those.

Michael Hardy
  • 1