16

I'd like to prove to my (undergraduate, not math-major) students that $$ \lim_{n\to\infty} \frac{1}{n^3}\sum_{k=1}^n k^2 =\frac{1}{3}, $$ to later show them that this can be interpreted as taking Riemann sums for the integral of $x^2$. Of course I could pull out of my hat the formula $\sum_{k=1}^n k^2 = \frac{n(n+1)(2n+1)}{6}$, which makes it obvious, or start from the telescopic sum $$\sum_{k=1}^n ((k+1)^3-k^3) $$ and do some algebra. Neither of them sounds very convincing to me, since they will be new ideas for them, not immediate to grasp, and this should not be the central point of my lecture.

Is there a simpler way to work out this limit, without going through a proof for the value of the sum?

Federico Poloni
  • 3,465
  • 2
    A very rough heuristic would replace the $k^2$ by $\frac{n^2}{2}$ so that $$\sum_{k=1}^nk^2\approx\sum_{k=1}^n\frac{n^2}{2}= n\cdot\frac{n^2}{2}=\frac{n^3}{2}.$$

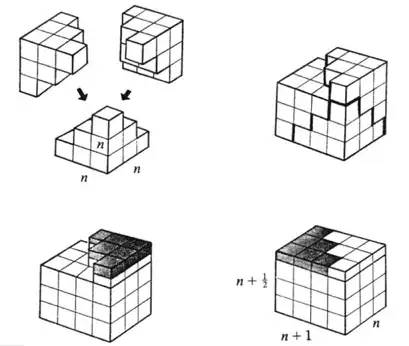
    That would be the why the $n^3$ makes an appearance.

     – JP McCarthy Mar 19 '14 at 13:26
  • 4
    If you're not working on this being particularly rigorous, you could interpret the sum as a square pyramid, and then quote the volume for such a shape. – preferred_anon Mar 19 '14 at 13:27
  • 1
    Also, you could just put numbers in - the limit converges pretty quickly. – preferred_anon Mar 19 '14 at 13:38
  • @DanielLittlewood I like your suggestions. If you formulate them as an answer, you'll have my upvote. – Federico Poloni Mar 19 '14 at 13:41
  • @FedericoPoloni Done, glad to be of help. – preferred_anon Mar 19 '14 at 13:56
  • The sum $1^2+2^2+\ldots+n^2$ has been discussed here many times. If you look at the answers here or the ones linked in the "linked" sidebar on that page, you will probably find something suitable. – MJD Mar 19 '14 at 14:40
  • @MJD I don't think it's the same question. I would like to find a quick proof for that limit without going through a whole proof of the closed form for the sum. – Federico Poloni Mar 19 '14 at 15:17
  • @FedericoPoloni I didn't say it was the same question; that's why I didn't vote to close your question as a duplicate. I was only trying to helpfully point out that this has been discussed here many times, and that, after discarding the proofs using the Snorfus quasisymmetric tensor theorem or whatever, there is probably something you will find useful. For example, the currently top-voted answer in this thread has already appeared here. – MJD Mar 19 '14 at 15:29

4 Answers4

17

enter image description here

${ }$

Community
  • 1
Bruno Joyal
  • 54,711
  • 2
    Nice. This also answers why formula of volumes of pyramids also include 1/3 in them instead of going through the integral. Easier to explain for secondary school! – user88595 Mar 19 '14 at 13:41
4

The limit is suitable for Stolz-Cesaro: $$ \lim_{n\to\infty}{1^2+2^2+\cdots+n^2\over n^3}= \lim_{n\to\infty}{(n+1)^2\over (n+1)^3-n^3}= \lim_{n\to\infty}{n^2+2n+1\over 3n^2+3n+1}={1\over 3}. $$ In fact, repeating the trick with $\sum_{k=1}^n k^2 -\frac{n^3}{3}$, you can calculate the coefficient of $n^2$ in $\sum_{k=1}^n k^2$... until the full formula.

Martín-Blas Pérez Pinilla
  • 41,546
  • 4
  • 46
  • 89
3

There are a couple of ways to make this limit seem intuitive. The sum of the squares can be interpreted as a square pyramid; the volume of such a pyramid is approximately $\frac{1}3 n^{3}$.

Another method could be to just calculate some of the partial sums. For example,
$$\frac{\sum_{k=1}^{10}k^{2}}{10^{3}}=0.385 \approx 1/3$$

preferred_anon
  • 17,121
  • Other good answers in the thread, but this one seems the most practical approach to me, so I am accepting this one. I am all for creative proofs of that identity, but I'd like to have something that the bottom 50% of the class can understand. – Federico Poloni Mar 22 '14 at 08:01
2

\begin{align*} 2\sum_{k=1}^n k^2 & = \sum_{k=1}^n k^2 + \sum_{k=1}^n(n-k+1)^2 \\ \\ & \approx \sum_{k=1}^n (n-k)^2 - (ik)^2 \\ & = \sum_{k=1}^n (n-(1+i)k)(n+(-i-1)k) \\ & \approx \sum_{k=1}^n(n-ik)^2 \end{align*}

Taking the real part

\begin{align*} 2\sum_{k=1}^n k^2 & \approx \sum_{k=1}^nn^2 - \sum_{k=1}^nk^2 \end{align*} and so \begin{align*} \sum_{k=1}^n k^2 & \approx \frac{n^3}{3} \end{align*}

Jack Rousseau
  • 1,198