What's the intuitive explanation that the volume of a solid is $\frac{1}{3} A_{base} h$?

Question

I can see why the area of a triangle is $A = \frac{1}{2} bh$ because it's half of a rectangle with sides $b$ and $h$, but I fail to see the intuitive explanation for this general volume formula. (Yes, I am aware it doesn't work for everything). If I were to take the same intuition and compare the pyramid to the prism, I don't see how the ratio of their volumes is $1$ to $3$ -- there's no obvious "fitting" of one into the other.

You can cut a prism into three pyramids, with equal height and base-area. — Lucian, Mar 11 '14 at 21:59

score 2 · Accepted Answer · answered Mar 11 '14 at 22:09

2

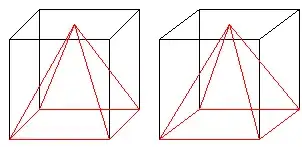
enter image description here

Examine this picture. If I wanted to fill the rest of the cube, I could need two more pyramids, each one cut in half vertically and placed on a sloping face of the drawn pyramid.

answered Mar 11 '14 at 22:09

Stella Biderman

31,155

score 2 · Answer 2 · answered Mar 11 '14 at 22:11

Take a cube of side $s$. It has volume $s^3$. Take the very center point and draw lines from each corner into the very center. This decomposes the cube into $6$ pyramids, one for each side of the original cube (they share a common tip).

Each pyramid must have volume $s^3/6$, since there are $6$ of them and they all have the same shape.

Each pyramid has base $b = s^2$ and height $h = s/2$. As we wanted to show, $\frac{1}{3}bh = s^3/6$.

(Whenever I try to cut a cube into 3 pyramids I run into visualization problems, so the 6-pyramid construction is much more intuitively clear to me.)

What's the intuitive explanation that the volume of a solid is $\frac{1}{3} A_{base} h$?

2 Answers2