6

We are given a circle with N randomly allocated points on it. Task is to find a chance that all N points lie on the one half of circle.

I have drafted some solution:
1. Since there are no way to put two points on circle, so that they were not on the same half-circle, $P_1$ and $P_2$ picked randomly and didn't affect the chance. So, required probability is:
$P(P_3) \cdot P(P_4)\: \cdot ... \cdot P(P_n)$, where $P(P_i)$ is the chance that i-th point lays on the proper half of circle.
2. Let's visualize what's $P(P_3)$, $P(P_4)$ look like:
Grey sector highlights forbidden part of circle.
It's obvious from pictures, that $P(P_i)$ approaching 0.5 as point amount increases
pp2 pp3
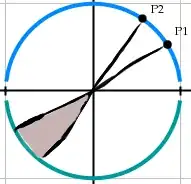
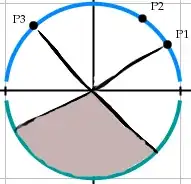
For this specific example, we could write: $P(P_3) = 1 - \frac {\Delta(\theta_2,\theta_1)} {2\pi}$ $P(P_4) = 1 - \frac {\Delta(\theta_3,\theta_1)} {2\pi}$.
3. Then if we generalize, $P(P_i) = 1 - \frac {\Delta_i} {2\pi}$, where $\Delta_i$ is a difference of angles of the most distant points.
And I'm understand that here I should introduce some generalized formula but I don't see it and don't want to make guesses. So I would appreciate any help.

Gilles Bonnet
  • 2,043
Dmitri K
  • 1,401
  • 1
    But the second point could land anywhere, and still be within a half circle of the first. If it lands at an angle $\theta$ from the first point, the third point has a chance of $1-\dfrac{\theta}{2 \pi}$ of landing acceptably. – Neil W Mar 11 '14 at 14:13
  • Any point could define a specific half circle and after that $n-1$ points have to lie on it. That means $1/2$ for every point. And finally $p=n/2^{n-1}$. – sas Mar 13 '14 at 17:24
  • @StevenStadnicki: We can now again vote to close; I did. – Marc van Leeuwen Mar 21 '14 at 10:37

3 Answers3

4

A suitable discretization of the problem is the following: we count in how many ways we can choose $n-1$ integers $i_1,\ldots,i_{n-1}$ such that $0=i_0\leq i_1\leq i_2\leq\ldots\leq i_{n-1}\leq i_n=2mn$ and for every $k\in[1,n]$ we have $i_{k}-i_{k-1}< mn$. This number is equal to the coefficient of the monomial $x^{2mn}$ in the product $$(1+x+\ldots+x^{mn-1})^n = \left(\frac{1-x^{mn}}{1-x}\right)^n=$$ $$=\left(1-nx^{mn}+\binom{n}{2}x^{2mn}-\ldots\right)\cdot \sum_{j=0}^{+\infty}\binom{n+j-1}{j}x^j,$$ hence it is equal to: $$\binom{n}{2}-n\binom{mn+n-1}{n-1}+\binom{2mn+n-1}{n-1},\tag{1}$$ while the number of choices that satisfy only $0=i_0\leq i_1\leq i_2\leq\ldots\leq i_{n-1}\leq i_n=2mn$ is equal to the coefficient of $x^{2mn}$ in the product $\frac{1}{(1-x)^n}$, i.e. the last term of $(1)$. So the probability that a sequence $0=i_0\leq i_1\leq i_2\leq\ldots\leq i_{n-1}\leq i_n=2mn$ has at least one index $k\in[1,n]$ such that $i_k-i_{k+1}\geq mn$ is equal to: $$\frac{n\binom{mn+n-1}{n-1}-\binom{n}{2}}{\binom{2mn+n-1}{n-1}}.\tag{2}$$ Taking the limit of $(2)$ with $m$ that goes to infinity gives that the probability $H_n$ for $n$ randomly chosen points on a circle to lie in the same half-circle. We have: $$ H_2 = 1, \quad H_3=\frac{3}{4},\quad H_4=\frac{1}{2},\quad H_5=\frac{5}{16},\quad H_n=\frac{2n}{2^n}.$$

Jack D'Aurizio
  • 353,855
  • 1
    As it was mentioned earlier, question turned out to be a duplicate. So thank you for answering any way. I found about duplicate after bounty was started, so I'm going to accept your answer and pay bounty to you. I have got some questions, thought. Would you clarify some points about your solution? It's very possible that I would be obliged to solve similar problems later, so I want to build solid understanding. I seem to get yours 'suitable discretization of the problem', but what x means it that case and how we come up with $(1 + x + ... x^{mn-1})^n$? – Dmitri K Mar 19 '14 at 12:10
  • For the first part, I slightly change the distribution: instead of having a uniform distribution over $S^1$, I take an uniform distribution over $2mn$ equally spaced points on $S^1$, then solve the combinatorial problem ("broken stick problem"). For the second part, just read the exponent of the monomial you choose in the $j$-th factor of $(1+x+\ldots)\cdot\ldots\cdot(1+x+\ldots)=(1+x+\ldots)^n$ as the difference $i_j-i_{j-1}$. – Jack D'Aurizio Mar 19 '14 at 12:20
  • Every difference has to be bounded by $mn$ and the sum of such differences must be equal to $2mn$, so you end with $$x^{2mn}^n,$$ as stated. – Jack D'Aurizio Mar 19 '14 at 12:21
  • I see that you already spent plenty of time to that answer, so thank you for keeping helping. I'm ashamed to admit, that I'm completely lost. What x variable stands for? Also I don't get: 1. How we get initial sequence. 2. How we got from $(\frac {1 - x^{mn}} {1-x})^n$ to the next expression. – Dmitri K Mar 19 '14 at 13:35
  • The variable $x$ stands for nothing, it is just the usual analytic-combinatorics enumerating technique in terms of generating functions. For instance, if you want to count in how many ways you can write $72$ as a sum of twenty positive integers less than five (here I mean $2+3+4+\ldots$,$2+4+3+\ldots$,$3+2+4+\ldots$ count for three), you just have to look at the coefficient of $x^{72}$ in $(x+x^2+x^3+x^4)^{20}$. – Jack D'Aurizio Mar 20 '14 at 12:13
  • Now $\left(\frac{1-x^{mn}}{1-x}\right)^n$ is just the product between the polynomial $(1-x^{mn})^n$ and the analytic function $\frac{1}{(1-x)^n}$. Take the Taylor series of both function in $x=0$, then read the product as a (Cauchy) product between power series. – Jack D'Aurizio Mar 20 '14 at 12:16
  • Moreover, there is an obvious bijection between the initial sequence $0=i_0,i_1,\ldots,i_{n-1}$ and the choice of the following points on $S^1$: $1=e^{\frac{\pi i i_0}{mn}},e^{\frac{\pi i i_1}{mn}},\ldots,e^{\frac{\pi i i_{n-1}}{mn}}$. – Jack D'Aurizio Mar 20 '14 at 12:25
0

This is not correct if which half circle is not specified at the start. Say the next point is at $\frac {2\pi}3$ radians. Your calculation says it has failed, but there is a half circle that contains both points-the one from $0$ to $\pi$, for example. The second point will always be within some half circle of the first. The hard part comes with the third point. Continuing my example, it could be anywhere from $-\frac \pi 3$ to $\pi$ radians, giving a chance of $\frac 23$ that the three points are in a half circle. Leaving the example, the third point is disallowed a range that matches the distance between the first two points. That is general: each point is disallowed an amount of the circle that is the range of the existing batch of points. This doesn't solve the problem.

Ross Millikan
  • 374,822
0

(This is along the answers found here: Probability that n points on a circle are in one semicircle)

Consider one of the points $x_k\in{\mathbb R}/{\mathbb Z}$. The probability that to the right of this point an interval of length ${1\over2}$ is free of other points $x_l$ comes to $2^{-(n-1)}$. Therefore the expected number $E$ of points $x_k$ with this property is given by $E=n\>2^{-(n-1)}$.

On the other hand, denote by $p_k$ the probability that we find exactly $k$ subintervals of length $\geq{1\over2}$. Then $E=\sum_{k\geq 0} k\>p_k$. As obviously $p_k=0$ when $k\geq2$ it follows that $$p_1=E={n\over 2^{n-1}}\ .$$

(This argument can also be used when ${1\over2}$ is replaced by a larger value, but not for a value $<{1\over2}$, since then $p_2>0$.)

The case $n=3$ can be handled in the following simple way: The first two points have a distance $t\geq0$ which is uniformly distributed in $\bigl[0,{1\over2}\bigr]$. Given these points the third point has a "forbidden range" of length $t$, so that we obtain $$p_1=\int_0^{1/2} (1-t)\>2dt={3\over4}\ .$$

Community
  • 1
Christian Blatter
  • 226,825