Please, can you help me to find the limit of the example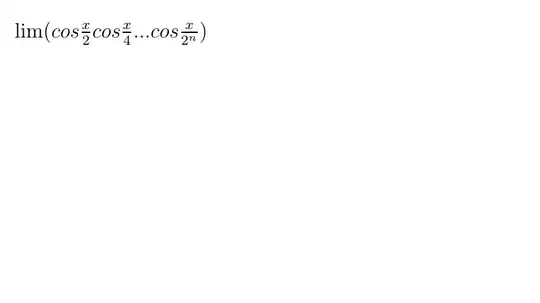
where n goes to infinity ?
Please, can you help me to find the limit of the example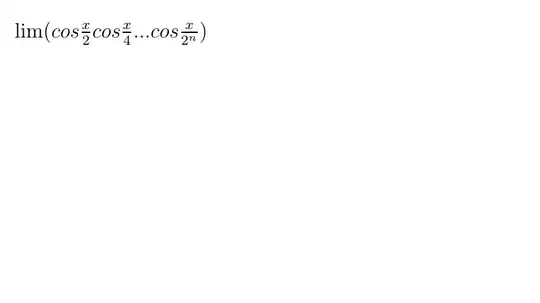
where n goes to infinity ?
Hint: write cos(x/2) = sinx/(2sin(x/2)), and cos(x/4) = sin(x/2)/(2sin(x/4)), etc...
The answer is $\frac{\sin x}{x}$.
See to this question's #1 answer: $\prod_{k=3}^{\infty} 1 - \tan( \pi/2^k)^4$
Just for your information (since you received good answers for the limit), the product from $i=1$ to $i=n$ of $\cos \left(2^{-i} x\right)$ has a closed form which is $$2^{-n} \sin (x) \csc \left(2^{-n} x\right)$$