Proof that an automaton stops

Question

I discovered an automaton that produced interesting, random-seeming patterns.

The rule was as follows. Given a grid of points, some occupied and some not, and a current point and a previous point; change the current point to the unoccupied point one knight's move (two steps in one direction and one in the other) clockwise from the previous jump (or two if that point is occupied, or three, and so on). Then change the previous point to the old current point, and add the current point to the set of occupied points.

Here are some pictures of the automaton at various stages with no points initially occupied:

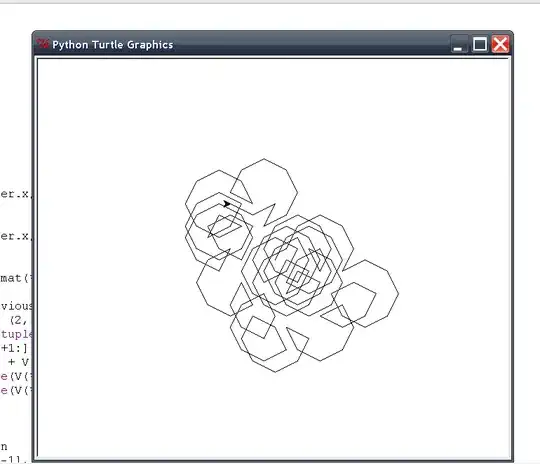
And here is the updated code used to generate them:

import turtle
import time

CELL_WIDTH = 8

class V:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def __iter__(self):
        yield self.x
        yield self.y

    def __add__(self, other):
        return V(self.x + other.x, self.y + other.y)

    def __sub__(self, other):
        return V(self.x - other.x, self.y - other.y)

    def __str__(self):
        return "({}, {})".format(*self)

def move(moves, position, previous, possible_moves, limit):
    c = 0
    while True:
        c += 1
        if c > limit:
            return None
        p = possible_moves.index(tuple(V(*position) - V(*previous)))
        for m in possible_moves[p+1:] + possible_moves[:p+1]:
            if tuple(V(*position) + V(*m)) not in moves:
                moves.append(tuple(V(*position) + V(*m)))
                turtle.goto(*tuple(V(*(8 * i for i in position)) + V(*(8 * i for i in m))))
                position, previous = moves[-1], position
                break
        else:
            turtle.reset()
            return moves, position

def generate(x, y):
    return ((x, y), (y, x), (y, -x), (x, -y), (-x, -y), (-y, -x), (-y, x), (-x, y))

original  = generate(1, 2)
onethree  = generate(1, 3)
onefour   = generate(1, 4)
onefive   = generate(1, 5)
onesix    = generate(1, 6)
twothree  = generate(2, 3)
twofive   = generate(2, 5)
threefour = generate(3, 4)
threefive = generate(3, 5)
fourfive  = generate(4, 5)

if __name__ == "__main__":
    turtle.speed(0)
    for thing in (original, onefive, onesix):
        for i in thing[:2]:
            result = move([(0, 0)], (0, 0), i, thing, 10000)
            if result is None:
                print("Move limit reached")
            else:
                positions, last = result
                print(len(positions))
        print()

The automaton does stop after about 369 or 515 steps. However, I only know this because I ran it. How would I go about proving that it does stop in another way, or prove that it stops with any initial finite set of occupied points? Also, has this (or a very similar) automaton been studied before?

Edit: as per magdiragdag's suggestion, I've run it again with different steps:

Step         Result
(2, 1)       Stops at 369 or 515
(3, 1)       Stops at 369 or 515
(4, 1)       Stops at 822 or doesn't stop at all (the pattern appears to repeat indefinitely)
(5, 1)       Stops at 104 or 505
(6, 1)       Stops at 724 or 1600
(7, 1)       Stops at 134 or 876
(8, 1)       Stops at 1746 or 1768
(9, 1)       Stops at 383 or 585
(3, 2)       Stops at 104 or 505
(4, 3)       Stops at 134 or 876
(5, 2)       Stops at 547 or 693
(5, 3)       Stops at 822, or doesn't seem to at all (similar pattern to (4, 1) but a different direction)
(5, 4)       Stops at 383 or 585
(7, 5)       Stops at 724 or 1600

Some jumps can obviously be reduced to others ($(4, 2)$ is the same as $(2, 1)$ etc). Some other jumps also appear to produce the same results:

(1, 2) and (1, 3)       515 or 369
(1, 3) and (1, 2)       515 or 369
(1, 4) and (3, 5)       822 or infinite
(1, 5) and (2, 3)       104 or 505
(1, 6) and (5, 7)       1600 or 724
(1, 7) and (3, 4)       134 or 876
(1, 8) and (7, 9)       1746 or 1768
(1, 9) and (4, 5)       383 or 585
(1, 10) and (9, 11)     1769 or 1769
(1, 11) and (5, 6)      1574 or 824
(1, 12) and  (11, 13)   1769 or 1769
(1, 13) and (6, 7)      1909 or 1557

(2, 1) and (1, 3)       515 or 369
(2, 3) and (1, 5)       104 or 505
(2, 5) and (3, 7)       547 or 693
(2, 7) and (5, 9)       1562 or 1027
(2, 9) and (7, 11)      921 or 1401
(2, 11) and (9, 13)     1769 or 1769

(1, 13) and (6, 7)      1909 or 1557
(3, 13) and (5, 8)      1439 or 2724
(5, 13) and (4, 9)      930 or 1808
(7, 13) and (3, 10)     921 or 1769
(9, 13) and (2, 11)     1769 or 1769
(11, 13) and (1, 12)    1769 or 1769

(1, 11) and (5, 6)      1574 or 824
(3, 11) and (4, 7)      1813 or 2065   
(5, 11) and (3, 8)      1629 or 964
(7, 11) and (2, 9)      921 or 1401
(9, 11) and (1, 10)     1769 or 1769

(8, 9)                  1769 or 1769

(1, 10), (7, 10), (9, 10), (11, 10) and (13, 10)                      1769 or 1769
(2, 11), (4, 11), (6, 11), (8, 11), (9, 11), (10, 11) and (12, 11)    1769 or 1769
(1, 12), (5, 12), (7, 12), (11, 12), (13, 12) and (25, 12)            1769 or 1769
(2, 13), (4, 13), (6, 13), (8, 13), (9, 13), (10, 13) and (12, 13)    1769 or 1769

(29, 41)                1769 or 1769

I noticed several patterns in these results.

Let $S(jump)$ denote the stopping time of a jump (e.g. $S(1, 2) = 515\ or\ 369$).

$S(1, x) = S(y, z)$, where $x$ is odd, and $y$ and $z$ are two numbers that add to make $x$, and have a difference of 1.

$S(1, x) = S(x-1, x+1)$, where $x$ is even.

$S(2, x) = S(|x-2|, x+2)$, where $x$ is odd.

From the above two results, it seems possible that $S(n, x) = S(|x-n|, x+n)$ where $x$ is even if $n$ is odd and vice versa (at least for certain values of $n$). I will test this later.

$S(13, x) = S(7-((x+1) / 2), x + (7-((x+1) / 2)))$ where $x$ is odd.

$S(11, x) = S(6-((x+1) / 2), x + (6-((x+1) / 2)))$ where $x$ is odd.

From the above two results, it seems possible that $S(n-1, x) = S((n/2)-((x+1) / 2), x + ((n/2)-((x+1) / 2)))$ where $x$ is odd (at least for certain values of $n$). I will test this later.

A lot of jumps stop at 1769:

$S(10, x)$ where $x$ and 10 are coprime. $S(11, x)$ where $x$ is composite. $S(12, x)$ where $x$ and 12 are coprime. $S(13, x)$ where $x$ is composite.

This suggests that $S(n, x)$ stops at 1769 when $n$ is even and $n$ and $x$ are coprime, and when $n$ is odd and $x$ is composite.

Above a certain point, all jumps seem to stop at 1769. All these jumps seem to have similar patterns.

From a brief search on Wolfram Alpha, I can't see any connections between the number of steps it takes jumps to stop, or anything overly remarkable about the number 1769, which seems to appear a lot.

Answer 1

Firstly here is some data for $S(x,y)$:

    1          2          3          4          5          6          7          8          9          10         11         12         13         14         
  -------------------------------------------------------------------------------------------------------------------------------------------------------
1 |
2 | 515 |369  
3 | 369 |515   104 |505  
4 | 822 |inf   515 |369   134 |876  
5 | 505 |104   547 |693   inf |822   383 |585  
6 | 1600|724   369 |515   515 |369   104 |505   1574|824  
7 | 876 |134   1562|1027  693 |547   1813|2065  724 |1600  1909|1557 
8 | 1746|1768  822 |inf   1629|964   515 |369   1439|2724  134 |876   1885|2493 
9 | 585 |383   921 |1401  369 |515   930 |1808  1027|1562  104 |505   1768|1746  1769|1769 
10| 1769|1769  505 |104   921 |1769  547 |693   515 |369   inf |822   1769|1769  383 |585   1769|1769 
11| 824 |1574  1769|1769  2065|1813  1769|1769  964 |1629  1769|1769  1401|921   1769|1769  1769|1769  1769|1769 
12| 1769|1769  1600|724   822 |inf   369 |515   1769|1769  515 |369   1769|1769  104 |505   134 |876   1574|824   1769|1769 
13| 1557|1909  1769|1769  2724|1439  1769|1769  1808|930   1769|1769  1769|921   1769|1769  1769|1769  1769|1769  1769|1769  1769|1769 
14| 1769|1769  876 |134   1769|1769  1562|1027  1769|1769  693 |547   515 |369   1813|2065  1769|1769  724 |1600  1769|1769  1909|1557  1769|1769 

It is a relatively obvious result that $S(x,y) = S(cx,cy)$ for any integer c, because you are effectively just making the grid larger.

As the author touched on, it does indeed appear to be the case that

$S(x, y) = S(x+y, x-y)$ for all x,y such that $x\perp y$ (and assuming x > y)

and reversed...

$S(x,y) = S((x+y)/2,(x-y)/2)$

From this we can see that $S(x,y)$ will be equal to a result obtained in a previous row if x+y is even (or if x and y are not coprime)

Up to $y=9$, every single value of $S(x,y)$ for x,y that do not fall into the above two categories was a result not previously obtained. However an examination of the data will reveal that at $y=10$, the number 1769 begins to appear to be the result of every single one of these. I have no idea why this rather abrupt change occurs, but have confirmed that there are no new results for any $9 < y < 100$. If it is the case that the pattern continues indefinitely, as it certainly seems to, then the only divergent x,y would be those with ratios $1:4$ or $3:5$.

(Notice how applying the pattern above a second time yields $S(x+y,x-y) = S(2x,2y)$, implying that a result will only be shared by x,y values of two possible ratios.)

Though this is far from a proof, (I didn't even prove the pattern for coprime x,y), all the data does seem to point very strongly toward there being no new results for $y \geq 10$. I would be interested in a proof of the pattern mentioned or of the 1769 occurrences. (I may attempt the former a bit later but I feel as if the latter is probably very difficult)

Update

After a bit of work I think I can demonstrate in a relatively rigorous way that $S(x,y) = S(x+y,x-y)$ for all x,y such that $x \perp y$.

To begin, see the following two images which display $S(3,2)$ and $S(5,1)$

The numbers show the possible positions after n moves. The yellow squares are ones which may contain even numbers and the red squares are those that contain odd numbers. It can be seen that the checkerboard pattern shown in $S(3,2)$ is one which will apply for any x,y such that x-y is odd, while the pattern below applies when x-y is even. Given this, these patterns and their properties are extensible beyond the example given.

Notice how the two grids are equivalent to each other rotated 45° (by, for example, taking any every other diagonal of the second and mapping it to a row in the first). Indeed, when applying a 45° rotation on $(x,y)$ we obtain

$x' = x\cos(45) - y\sin(45)=\frac{x}{\sqrt2} - \frac{y}{\sqrt2}\\ y' = x\sin(45) + y\cos(45)=\frac{x}{\sqrt2} + \frac{y}{\sqrt2}$

and when normalizing to integers by multiplying by $\sqrt{2}$ (maintaining the 45° difference)

$x',y' = x-y,x+y$

(they may appear switched, but it is clear that $S(x,y) = S(y,x)$)

This demonstrates the symmetry these movements have over rotations of 45°, in particular that the movements of $S(x+y,x-y)$ can be 'simplified' to the movements of $S(x,y)$. This took me a bit of thinking and sketching out but the reason behind why it works is really quite elegant. In addition to the obvious symmetries the movements possess over scaling, reflecting, and rotating by 90°, there is a more subtle symmetry over 45° rotation.

Another Update

Here is an explanation for 1769 occurring for every coprime x,y for $y\geq 10$. Firstly to avoid ambiguity I will refer to the input values as a and b, and the actual positions at any given time as x and y.

This automation is one which changes its behavior when $x_0,y_0 = x_1,y_1$ where $(x_0,y_0)$ is the current position and $(x_1,y_1)$ is any previous position. Any x and y values in the series of positions visited by $S(a,b)$ may be written as follows:

$x = n_xa + m_xb\\ y = n_ya + m_yb\\ n_x,m_x,n_y,m_y \in \mathbb{Z}$

Every time a move is made, either both $n_x$ and $m_y$ will change by one, or both $m_x$ and $n_y$ will change by one. For example if we have $a=2$ and $b=5$, $n_x$ would represent how many times it has moved horizontally 2 units and $m_x$ would represent how many times it has moved horizontally 5 units (positive for left and negative for right).

The condition that $x_0,y_0 = x_1,y_1$ occurs when

$n_{x0}a + m_{x0}b = n_{x1}a + m_{x1}b\\ n_{y0}a + m_{y0}b = n_{y1}a + m_{y1}b$

or more generally

$n_0a + m_0b = n_1a + m_1b$

This relationship can be written as

$n_0 - n_1 = C \frac{b}{\gcd(a,b)}\\ m_0 - m_1 = -C \frac{a}{\gcd(a,b)}\\ C \in \mathbb{Z}$

Note that the trivial case $C=0$ (or $(n_0,m_0)=(n_1,m_1)$) does not depend on the values of a and b, and will occur at the same n and m values no matter the input.

Other than those involving the trivial case, this shows that the collision between any two positions would have to have n values whose difference was at least $\frac{b}{\gcd(a,b)}$ and m values whose difference was at least $\frac{a}{\gcd(a,b)}$ (for both x and y components).

Since $\gcd(a,b) = 1$ for $a \perp b$, it is clear that $\frac{b}{\gcd(a,b)} = b$ for coprime a and b. This means that for $S(a,b)$ the minimum difference between the n values for non-trivial collisions would be $b$. Because every move can only change n or m by one, for sufficiently large $b$, $S(a,b)$ may actually terminate before a difference this size between any two n values is reached. In addition it is clear that if the sequence terminated before this difference was reached for some $b$, it would also do so for any higher value of $b$. This means that once a row is reached in which said termination occurs, it will occur for all rows following.

This, along with what was demonstrated previously shows that no new results will occur for sufficiently large b ($b\geq 10$) and that the only non-terminating inputs are those with ratios $1:4$ and $3:5$.

A couple things should be noted on this. While I only discussed the n values in the above paragraph, since any collision requires both the n values and the m values to match, it is sufficient to show that the n values will never match in a non-trivial way for sufficiently large b. Additionally, many trivial collisions ($C=0$) do still occur for sufficiently high rows, however as explained above, since these collisions occur at equal n and m values regardless of the given a and b, they exhibit the same pattern for any a and b values (as long as the pattern is not disrupted by non-trivial collisions which are dependent on the a and b values).

Wow, I have to admit I didn't plan on spending as much time on this as I did, but thanks for a great question and something to do with my weekend. This was a pretty difficult problem, and I am actually somewhat surprised that I was able to obtain a definitive answer. If anyone has the patience to read the whole thing I would love to hear thoughts on this method (hope I didn't make any mistakes!).