For which n can $a^{2}+(a+n)^{2}=c^{2}$ be solved, where $a,b,c,n$ are positive integers? I have found solutions for $n=1,7,17,23,31,41,47,79,89$ and for multiples of $7,17,23$... Are there infinitely many prime $n$ for which it is solvable?
- 26,355
- 10,200
-
The title says "primitive", so $GCD(a,n,c)=1$ is assumed? – pharmine Oct 07 '11 at 12:35
-
2@Angela: Very interesting question! – rubik Oct 07 '11 at 12:39
-
A paper with some useful info about this question is Delano Wegener. Primitive Pythagorean triples with sum or difference of legs equal to a prime. Wegener proves that your equation is solvable for prime $p$ iff $p=\pm1\mod 8$. – Rosie F Mar 29 '20 at 17:32
4 Answers
The general primitive solution to $x^2+y^2 = z^2$ is given by: $x=u^2-v^2$, $y=2uv$, $z=u^2+v^2$, with $u,v$ relatively prime and not both odd.
For $(a,a+n,z)$ to be a primitive triple, we'd have to have a $(u,v)$ such that: $|u^2 - v^2 - 2uv| = n$. We can rewrite that as: $(u-v)^2 - 2v^2 = \pm n$
So, setting $w = u-v$, we want to find $(w,v)$ which are relatively prime and $w$ is odd, with:
$$w^2-2v^2 = \pm n$$
This means that $n$ must be odd.
In fact, we can use unique factorization in $\mathbb{Z}[\sqrt{2}]$ to show that $n$ can be any product of primes of the form $8k\pm 1$. Since there are infinitely many primes of the form $8k\pm 1$, the answer to your question is, "yes."
(Oh, and once you find one solution $(w,v)$ for a particular $n$, you can find infinitely many solutions for that $n$.)
- 177,126
-
For example, $-71 = w^2 - 2v^2$ has solution $(w,v)=(1,6)$. So $u=7$, $x=u^2-v^2 = 13$, $y=2uv=84$, and $z=u^2+v^2=85$, so $n=71$ has a solution with $a=13$. – Thomas Andrews Oct 07 '11 at 19:01
-
Explicitly, if $p^2 + (p+n)^2 = r^2$, then subsequent ones can be found as $q^2 + (q+n)^2 = (p+q+r+n)^2$, where $q = 3p+2r+n$. – Tito Piezas III Nov 25 '14 at 23:40
$2a^{2}+2na+n^{2}=c^{2}$ --> $a=-\frac{-n+\sqrt{2c^{2}-n^{2}}}{2}$ --> there are solutions iff $x^{2}+n^{2}=2c^{2}$ has solutions --> find the set of the squares of all integers 0 in the set such that $y=2x-n$ then there is a primitive pythagorean triple with a difference of n between legs, and also for any multiple An if n>1 since if $k^{2}\equiv x(\mod{n})$ then $(Ak)^{2} \equiv Ax(\mod{An})$ --> $Ay=2Ax-An$.
- 10,200
There are infinitely many Pythagorean triples where the difference between two legs is either $1$ or any of the infinite prime numbers $P\equiv\pm 1 \mod 8\quad$ taken to any non-zero power.
Under $100\quad P\in \{1,7, 17, 23, 31, 41, 47, 49, 71, 73, 79, 89, 97\}.\quad $ To find these, we begin with Euclid's formula $ \quad A=m^2-k^2,\quad B=2mk,\quad C=m^2+k^2\quad$ solve the $\quad (B-A)$ difference equation for $m$ and generate the $(m,k)$ values needed to feed Euclid's formula. Each iteration uses a seed $k$ which is either given or is the $m$-value of the previous iteration. Here is the formula for $P=1$ with a seed $k=1$. Note that $(m,k)$ are Pell numbers.
\begin{equation} \quad m=k+\sqrt{2k^2+(-1)^k} \end{equation} \begin{align*} k=1\space &\implies m=(1+\sqrt{2(1)^2+(-1)^1}\space)\big)=2\quad & F(2,1)=(3,4,5)\\ k=2\space &\implies m=(2+\sqrt{2(2)^2+(-1)^2}\space)\big)=5\quad & F(5,2)=(21,20,29)\\ k=5\space &\implies m=(5+\sqrt{2(5)^2+(-1)^5}\space)\big)=12\quad & F(12,5)=(119,120,169)\\ k=12\space &\implies m=(12+\sqrt{2(12)^2 (-1)^{12}}\space)\big)=29\quad & F(29,12)=(697,696,985) \end{align*}
For $P>1$, the formula is
\begin{equation}
m=k+\sqrt{2k^2\pm P}
\end{equation}
and there is more than one seed $(s)$ in a set $(k_1)$ each of which generates a subset of the entire set of triples for that difference. There is one more seed than the power $n$ of the prime number that is P. For example, $1$ is a zero power so there is $1$ seed.
$$P=1\implies k_1=\{s1\}=\{1\}\quad
P=7^1\implies k_1=\{s1,s2\}=\{2,1\}\\
P=343=7^3\implies k_1=\{s1,s2,s3, s4\}=\{14,16,3,7\}$$
The elements of $k_1$ are generated as follows.
\begin{equation} \end{equation} \begin{align*} \text{where}\quad s_i=\sqrt{\frac{j_i^2 + P}{2}} \\ &\text{for}\space\space\space 1 \le i \le \bigg\lceil\frac{(n+1)}{2}\bigg\rceil \space \land \space \space 1 \le j_i \le \lfloor\sqrt{X}\rfloor\\ \text{where}\space s_i=\sqrt{\frac{j_i^2-P}{2}} \\ &\text{for}\space \bigg\lceil\frac{(n+1)}{2}\bigg\rceil + 1 \le i \le (n+1)\space \land \space \lfloor\sqrt{P} +1 \rfloor \le j_i \le \lfloor\sqrt{2P}\rfloor \end{align*}
For example, we have $n=3, P=7^3=343\\$ \begin{align*} 1 \le & i \le 2 \space 1 \le & j \le \lfloor\sqrt{343}\rfloor=18 \space \\ s_1=\sqrt{\frac{7^2+343}{2}}=14\space\quad & s_2=\sqrt{\frac{13^2+343}{2}}=16 \\ 3 \le & i \le 4 \space 19 \le & j \le \lfloor\sqrt{2(343)}\rfloor=26 \space \\ s_3= \sqrt{\frac{19^2-343}{2}}=3 \quad & s_4=\sqrt{\frac{21^2-343}{2}}=7 \ \end{align*}
\begin{align*} s_1= 14\quad &14+\sqrt{2(14)^2-343}=21\quad &F(21,14)=(245,588,637)\\ &21+\sqrt{2(21)^2+343}=56\quad &F(56,21)=(2695,2352,3577)\\ s_2=16 \quad &16 +\sqrt{2(16)^2-343}=29\quad &F(29,16)=(585,928,1097)\\ &29 +\sqrt{2(29)^2-343}=74\quad &F(74,29)=(4635,4292,6317)\\ s_3=3 \quad &3+\sqrt{2(3)^2+343}=22\quad &F(22,3)=(475,132,493)\\ &22+\sqrt{2(22)^2+343}=47\quad &F(47,22)=(1725,2068,2693)\\ s_4=7 \quad &7 +\sqrt{2(7)^2+343}=28\quad &F(28,7)=(735,392,833)\\ &28+\sqrt{2(28)^2+343}=63\quad &F(63,28)=(3185,3528,4753)\\ \end{align*}
For $P=1$ These $(m,k)$-values may be generated directly using a Pell-related equation as follows. \begin{equation} m_n= \frac{(1 + \sqrt{2})^{n+1} - (1 - \sqrt{2})^{n+1}}{2\sqrt{2}}\qquad \qquad\qquad k_n= \frac{(1 + \sqrt{2})^n - (1 - \sqrt{2})^n}{2\sqrt{2}} \end{equation} For example
{\small
\begin{align*}
\frac{(1 + \sqrt{2})^{2} - (1 - \sqrt{2})^{2}}{2\sqrt{2}}=2 \quad
\frac{(1 + \sqrt{2})^1 - (1 - \sqrt{2})^1}{2\sqrt{2}}=1 \quad& F(2,1)=(3,4,5)\\
\frac{(1 + \sqrt{2})^{3} - (1 - \sqrt{2})^{3}}{2\sqrt{2}}=5 \quad
\frac{(1 + \sqrt{2})^2 - (1 - \sqrt{2})^2}{2\sqrt{2}}=2 \quad& F(5,2)=(21,20,29)\\
\frac{(1 + \sqrt{2})^{4} - (1 - \sqrt{2})^{4}}{2\sqrt{2}}=12 \quad
\frac{(1 + \sqrt{2})^3 - (1 - \sqrt{2})^3}{2\sqrt{2}}=5 \quad& F(12,5)=(119,120,169)\\
\frac{(1 + \sqrt{2})^{5} - (1 - \sqrt{2})^{5}}{2\sqrt{2}}=29 \quad
\frac{(1 + \sqrt{2})^4 - (1 - \sqrt{2})^4}{2\sqrt{2}}=12 \quad& F(29,12)=(697,696,985)
\end{align*}
}
- 6,338
-
https://math.stackexchange.com/questions/5540/k2k12-being-a-perfect-square-for-infinitely-many-k/700126#700126 there's a connection to Pell's equation. – individ Jan 10 '21 at 05:21
-
@ individ 59 I know about the Pell connection with $P=1$ and I have added such to my answer. Unfortunately, I have inconsistent luck with the ability to change font size in MathJax: Do you know how to make it \small or \footnotesize? – poetasis Jan 10 '21 at 06:24
If you solve expression for $n$ you get
$n=\sqrt{c^2-a^2}-a$, let's denote $b=\sqrt{c^2-a^2}$,so we have that $n=b-a$
Now,take look at picture bellow.Note that $AD=a$,and $BD=b-a=n$
If you change value of $b$ and keep $a$ to be constant you will get a infinite number of right triangles,and therefore infinite number of values of $n=b-a$,so answer is yes, there are infinitely many primes $n$ for which equation is solvable.
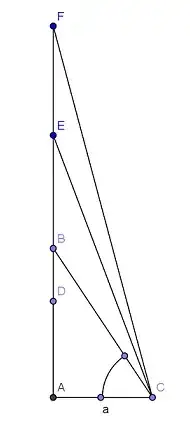
- 12,883
-
1Except that you don't know for which integer values of $b$ yield integer values of $c$. – Thomas Andrews Oct 07 '11 at 14:57
-
@Thomas,That's true,I have answered only on second part of the question...however, one can find one (a,b,n) triple and then for each different triple choose another b such that n becomes prime number – Pedja Oct 07 '11 at 15:18
-
1
-
@Thomas,I didn't say that this reasoning is correct for each prime number.I just pointed that there is infinitely many distinct (a,b,n) triples such that n is prime... – Pedja Oct 07 '11 at 15:48
-
This probably unnecessary at this point but, among primitive Pythagorean triples, the difference between the two legs is always a prime $P\equiv \pm 1 \mod 8\quad$ and I have shown how to find such triples in my recent answer. – poetasis Jan 09 '21 at 01:52
-
@poetasis Not quite. Each prime factor of this difference $n$ is $p=\pm1\mod 8$, but $n$ might not be prime. For example, there's $a=24, n=119=7\cdot 17, c=145$ which is primitive. – Rosie F Jan 04 '23 at 10:35