5


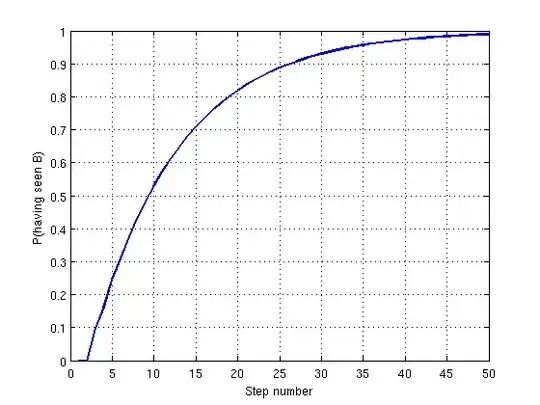
To get specific first off, it's about this graph:
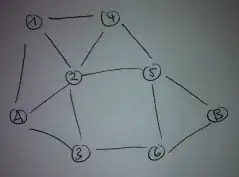
graph

I want to get from $A$ to $B$. Every edge has the same length (e. g. 1 m). The shortest walk from $A$ to $B$ is easily found ($A-2-5-B$ and $A-3-6-B$). But how can I calculate the average length of a walk and its probability, when I am navigating randomly through this graph (what is the length/probability of $n$ steps)? At every node, there is a chance of $p= \frac{1}{degree}$ to choose any next edge (also back, where I just came from). For example, there would be a chance of walking in circles for a long time, but probability decreases - also to get straight through.

I wrote a computer simulation to find a statistic answer: After a megaattempt (1000000 attempts), it averaged at about 20.329 edges for this specific graph here.

I'd also like to know how to calculate such things in general, of course ;)

Path vs. Walk: Some authors (e.g. Bondy and Murty 1976) use the term "walk" for a path in which vertices or edges may be repeated, and reserve the term "path" for what is here called a simple path. - https://en.wikipedia.org/wiki/Path_(graph_theory)

smci
  • 364
ste
  • 321

2 Answers2

3

It's difficult to claim an average because there exist many possible infinite length paths that never reach $B$. You may want instead to calculate the probability that you have reached $B$ after $n$ steps.

@draks ... is on to something, but if you're going to determine the probably that you have "seen" node $B$ after $n$ steps, then you definitely need to include the probability as weights in the adjacency matrix.

Question: For the given graph $G$, what is the probability of having seen node $B$ at the $n^{th}$ step?

Answer: Let us write the adjacency matrix of $G$ weighted with edge probabilities as $$M = \begin{bmatrix} 0 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} & 0 & 0 & 0 & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & 0 \\ \frac{1}{5} & \frac{1}{5} & 0 & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & 0 & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & 0 & \frac{1}{3} & 0 \\ 0 & \frac{1}{4} & \frac{1}{4} & 0 & 0 & \frac{1}{4} & 0 & \frac{1}{4} \\ 0 & 0 & \frac{1}{4} & 0 & \frac{1}{4} & 0 & \frac{1}{4} & \frac{1}{4} \\ 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & 0 & \frac{1}{3} \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 \\ \end{bmatrix}$$

Let $N$ be the matrix $M$ with the last row and column removed. Then the probability of having seen $B$ at step $n$ is then equal to 1 minus the sum of the first row of $N^{n}$ (because that is the row corresponding to the node we started from $A$).

Here's a pretty picture of how the probability changes as $n$ increases: Probability of having seen $B$ at step $n$

Carser
  • 3,400
1

Since the walk should stop at $B$, let $A$ be the adjacency matrix of your graph without the $B$ vertex. The powers of $A$, i.e. the matrix elements $(A^n)_{km}$ represent the number of ways from vertex $k$ to $m$.

We look at the elements $(A^n)_{05}$ and $(A^n)_{06}$, because with one more step we can reach $B$.

EDIT

If you need paths without backtracking, I think you can use this...

Community
  • 1
draks ...
  • 18,449