1

I'm doing a problem where my task is to determine whether a given function is continuous, piecewise continuous or piecewise smooth on interval $[-\pi, \pi]$. According to my book the function:

$$\sqrt[\leftroot{0}\uproot{0}3]{\sin(\theta)}$$

is continuous on that interval. Here is a graph of the function:

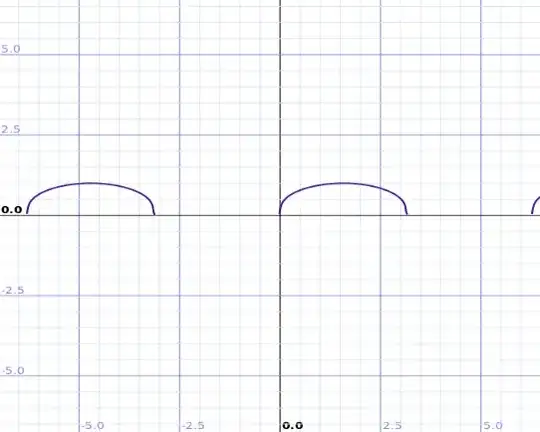
enter image description here

I can see that the function is continuous on the interval $[0, \pi]$ and not defined on the interval $(-\pi, 0)$. I have understood that continuity means that we can draw the graph "without lifting the pencil" at any point. But if I would draw the function $\sqrt[\leftroot{0}\uproot{0}3]{\sin(\theta)}$ on interval $[-\pi, \pi]$ then I would not have any gap on the interval $[0, \pi]$, but I would have a gap between the point $-\pi$ and the interval $[0, \pi]$. So is this then continuous or not on the interval $[-\pi, \pi]$?

jjepsuomi
  • 8,619
  • 1
    You only look at continuity on the interval $[0,\pi]$, and the point $-\pi$ is outside this interval. – Ulrik Mar 06 '14 at 07:47
  • +1 @Svinepels Thank you for your help. So the function is NOT then continuous on the interval $[-\pi, \pi]$? Because the question is: Is the given function continuous n the interval $[-\pi, \pi]$? =) – jjepsuomi Mar 06 '14 at 07:48
  • Any function is not continuous where it is undefined. – superAnnoyingUser Mar 06 '14 at 07:49
  • 1
    Obviously, the extension of the cube root as in $\sqrt[3]{x}=\text{sign}(x)\sqrt[3]{|x|}$ is intended in the task. So that $\sqrt[3]{-8}=-2$. -- And the function is Hölder-continuous with Hölder index $1/3$. – Lutz Lehmann Mar 06 '14 at 07:51
  • 1
    Your graph is not correct, since $\sin$ is defined on $\mathbb R$ and $\sqrt[3]{x}$ is defined on $\mathbb R$, so the composition $f(\theta)=\sqrt[3]{\sin(\theta)}$ is defined on $\mathbb R$. For example, $f(-\frac{\pi}{2})=\sqrt[3]{-1}=-1$.

    In addition, the claim that a continuous function is "drawn without lifting the pencil" (which is by the way, not a mathematical statement) is true only if f is continuous and defined on an interval.

     – Taladris Mar 06 '14 at 07:53
  • +1 @Taladris ah, you are correct =) I see now, I used online function grapher for this x) Guess the image got me confused =) – jjepsuomi Mar 06 '14 at 07:55
  • @Taladris: Make that Lipschitz continuous or rectifiable. One can not draw with a pencil a fractal curve with infinite length and wild oscillations. But such functions may still be Hölder continuous. – Lutz Lehmann Mar 06 '14 at 07:55
  • @LutzL: I don't understand your first comment. By definition, the cube root of $a$ is the only real number $x$ such that $x^3=a$. It exists an is unique for any real number $a$. Why would we need a generalization? We have directly $\sqrt[3]{-8}=-2$ since $(-2)^3=-8$. – Taladris Mar 06 '14 at 07:56
  • This is a recurring topic. The root functions in general are only defined for non-negative arguments. The odd-degree root functions have one natural extension to negative reals. But in complex numbers, the principal roots are chosen to have the smallest argument, so that, again, in the extension to the complex plane, $\sqrt[3]{-1}=\tfrac12(1+i\sqrt{3})$. This is, for instance, the standard result on Wolfram-Alpha and many other CAS. So one has to be specific which function to use – Lutz Lehmann Mar 06 '14 at 08:00
  • @LutzL: I don't understand why I could not define directly odd-degree root for real numbers, this extension looks useless to me. This is when extending from real numbers to complex ones than one has to be careful. Could you provide me a link to another topic? It may help me to understand.

    Thank you for the comment on the Holder example. I guess "the graph can be drawn without lifting the pencil" is usually a non mathematical but intuitive way to say that "the image of an interval a continuous function is connected".

     – Taladris Mar 06 '14 at 08:22
  • Last first: The examples discussed in the "pencil" context are usually at least piecewise continuous, so the necessity for epsilontic is often difficult to communicate. Links for the cube root topic: http://math.stackexchange.com/q/25528/115115, perhaps http://math.stackexchange.com/q/636415/115115 and http://math.stackexchange.com/q/556446/115115. And http://mathworld.wolfram.com/CubeRoot.html from from the first link. – Lutz Lehmann Mar 06 '14 at 08:49

1 Answers1

1

The cube root function is continuous in ${\Bbb R}$, $\sin$ is continuous in ${\Bbb R}$. Your function is continuous because is composition of two continuous functions.

Martín-Blas Pérez Pinilla
  • 41,546
  • 4
  • 46
  • 89
  • +1 Thank you for your help, I noticed my graph from online grapher is not correct as stated in the comments =) – jjepsuomi Mar 06 '14 at 07:56
  • By the way I'm curious, I have tried four different online graphers and they all give the same graph. I have used as my input the function $\sin(x)^{1/3}$, shouldn't this be the cubic root of $\sin(x)$? – jjepsuomi Mar 06 '14 at 08:07
  • 2
    Fractional powers of negative numbers are problematic for numerical computing. The computer can't tell the difference between $\alpha = 1/3$ and $\beta = \frac {33333333333333333}{100000000000000000}$. But a negative number to the power $\beta$ should be imaginary since $\beta$ has an even denominator. – Robert Israel Mar 06 '14 at 08:13
  • 2
    On the other hand, for symbolic computation, many computer algebra systems prefer the "principal branch" of non-integer powers, defined by $z^\alpha = \exp(\alpha \text{Log}(z))$. Thus in Maple, $(-1)^{1/3}$ is not $-1$ but $e^{i\pi/3}$. – Robert Israel Mar 06 '14 at 08:16
  • +1 Thank you again =) @RobertIsrael will keep that in mind =) – jjepsuomi Mar 06 '14 at 08:24
  • @RobertIsrael The symbolic program Maxima draws correctly the function: plot2d((sin(x))^(1/3),[x,-10,10]). Surely you can change the default branch in Maple/Mathematica... – Martín-Blas Pérez Pinilla Mar 06 '14 at 08:26
  • In Maple, surd(x,n) can be used instead of $x^{1/n}$. – Robert Israel Mar 07 '14 at 03:10