how to find nth term of different fibonacci series with golden ratio

Question

what i know :

if i want to find $Nth$ term of a fibonacci series like :

1   1   2   3   5   8   13  21 .......

then to find $6th$ term we use golden ratio like:

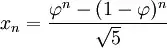
enter image description here

so it becomes like :

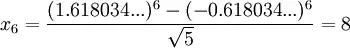
enter image description here

well and good.now

what i want to know :

what changes should i make in golden ratio or while applying it for different fibonacci series . For example :

1   6   7   13   20   33 .......

now if i want to find the 10th no. of above series then what changes should i do in golden ratio... now what is the value of X₁₀'s R.H.S(right hand side)

X₁₀ = ? (for this fibonacci series)

If you look at a derivation of Binet's formula using generating functions, then it should be clear how to generalize the result. — Bulberage, Mar 05 '14 at 21:53

score 2 · Accepted Answer · answered Mar 05 '14 at 21:51

2

In general, the solution of a recursion $a_n = A a_{n-1} + B a_{n-2}$ is of the form $a_n = C \lambda_1^n + D \lambda_2^n$, where $\lambda_{1,2}$ are the roots of $\lambda^2 - A \lambda - B = 0$. You can find $C$ and $D$ by plugging in $n=0$ and $n=1$.

For the Fibonacci sequence, one of $\lambda_{1,2}$ is equal to the golden ratio.

answered Mar 05 '14 at 21:51

user133281

16,073

cant get you,sorry ..can you explain with the example please – RbG Mar 05 '14 at 21:52
In your example, $A=B=1$ so the roots of the characteristic polynomial $\lambda^2 + \lambda + 1=0$ again equal the golden ratio $\phi$ and $1-\phi$. Hence the general term is $a_n = C \phi^n + D(1-\phi)^n$, where $C$ and $D$ can be determined from $a_0$ and $a_1$. – user133281 Mar 05 '14 at 21:54
for the next one a=6 and b=7 right??? – RbG Mar 05 '14 at 21:55
according to your solution it should be λ^2 - λ - 1 = 0 but you wrote λ^2 + λ + 1 = 0 ... why??? – RbG Mar 05 '14 at 21:58
You're right, should be $\lambda^2=\lambda+1$. – user133281 Mar 05 '14 at 22:34
how will i get C and D from a0 and a1 – RbG Mar 05 '14 at 22:38
1

Solve the system $C+D=a_0$, $C\phi + D(1-\phi) = a_1$. – user133281 Mar 05 '14 at 22:39

MJD · Answer 2 · 2014-03-05T22:42:08.310

If $s$ satisfies the recurrence $s_{n+2} = s_n + s_{n+1}$, and its first two terms are $s_0$ and $s_1$, then then $$s_i = s_0f_{i-1} + s_1f_i$$ for all $i$, where $f_n = 0, 1, 1, 2, 3, \ldots$ is the Fibonacci sequence.

For example, the sequence $a_i = 1, 6, 7, 13, 20, 33,\ldots $ is generated by $a_i = f_{i-1} + 6f_i$:

$$\begin{array}{r|rr|r} i & f_{i-1} & f_i & f_{i-1} + 6f_i \\\hline 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 6 \\ 2 & 1 & 1 & 7 \\ 3 & 1 & 2 & 13 \\ 4 & 2 & 3 & 20 \\ 5 & 3 & 5 & 33 \\ 6 & 5 & 8 & 53 \\ \end{array}$$

You already have a formula for $f_i$, which you can substitute into $f_{i-1} + 6f_i$ to get a formula for your sequence.

how to find nth term of different fibonacci series with golden ratio

2 Answers2