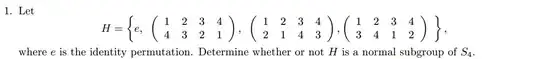
Do I really have to go through checking each and every left and right coset for this problem? Surely there must be a more efficient way that I don't know about?
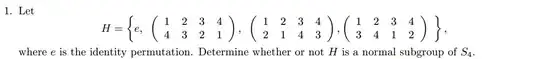
Do I really have to go through checking each and every left and right coset for this problem? Surely there must be a more efficient way that I don't know about?
Hint: Conjugating by a permutation doesn't change the cycle structure.
I'll use a slightly more efficient notation in answering your question, as it's the notation that most people use when discussing symmetric groups. This notation is called cycle notation. Instead of writing where every element goes, as you do above, we write only the action of a permutation on those elements of $\left\{1,\cdots,n\right\}$ for which it does not act by the identity. For instance, the element that sends 1 to 2, 2 to 1, 3 to 3, and 4 to 4 would be written $(12)$.
We want to understand whether $H=\left\{(0), (14)(23), (13)(24)\right\}$ defines a normal subgroup of $S_4$, as will turn out to be the case. One way of doing this is to check cosets as you stated. Since the order of $H$ is 4 there are 6 of them, so while it is tedious in this case it's certainly doable. On the other hand, we might imagine having to do this problem in a larger group where our patience for this sort of computation might be thin.
A subgroup $H\leq G$ is called normal when $H$ is invariant under conjugation by elements of $G$. Consider an arbitrary $\sigma,\tau\in S_n$ and suppose we want to study $\sigma\tau\sigma^{-1}$. As it turns out, there is a very simple description of how conjugation works in $S_n$, the cycles of $\sigma\tau\sigma^{-1}$ are exactly the cycles of $\tau$ where we act on the components by $\sigma$. As a short example, in $S_4$ if $\sigma = (12)$ and $\tau=(34)$ then $\sigma\tau\sigma^{-1} = (12)(34)(21) = (\sigma(3)\sigma(4))=(34)$.
Returning to our problem, we see that all the elements of $H$ have the form $(ab)(cd)$, so that their conjugates under any element $\sigma$ are $(\sigma(a)\sigma(b))(\sigma(c)\sigma(d))$. In $S_4$ it is not difficult to check (HW) that this also has the form of the product of transpositions, and further that all such transpositions are represented under conjugation.
$S_4$ has in some sense the most interesting normal subgroup structure of all the symmetric groups. After resolving the details in your argument, you might want to think about why this sort of computation doesn't work in $S_n$ for $n\neq 4$.