3

Possible Duplicate:
Is there a name for this strange solution to a quadratic equation involving a square root?

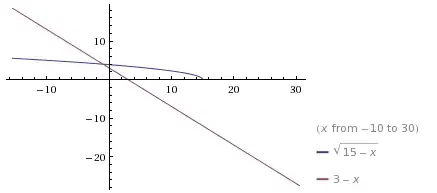
enter image description here

As you can see, they only cross once. By setting
$3-x=\sqrt{15-x}$
I manage somehow to find two possible values for x.
$3-x=(15-x)^2$
$(3-x)=(15-x)^{\frac{1}{2}}$
$(3-x)^2=((15-x)^{\frac{1}{2}})^2$
$9-6x+x^2=15-x$
$x^2-5x-6=0$
$x_1=6$ and $x_2=-1$
$y_1=3-6=-3$ and $y_2=3-(-1)=4.$
$(6,-3)$ and $(-1,4)$
Only $(-1,4)$ is a real intersection.
How is that this method of calculating the intersection allows me to find this false positive if you will?

Community
  • 1
Algific
  • 1,899
  • 1
    Not a duplicate, that question only asked for the name of the unwanted solution. This one is quite different. It also has the nice feature of including a picture, which enriches the analysis. – André Nicolas Oct 04 '11 at 00:51
  • The line in the question right after "two possible values", which says $3-x=(15-x)^2$ is wrong. The the two immediately below it are right. – Michael Hardy Oct 04 '11 at 00:53

2 Answers2

3

You started with the equation $$3-x=\sqrt{15-x},$$ and then squared both sides, obtaining the equation $$(3-x)^2=15-x.$$

Now suppose that you had started from the equation $$3-x=-\sqrt{15-x},$$ and squared both sides. Again you would get $$(3-x)^2=15-x.$$

How is the poor equation $(3-x)^2=15-x$ to know whether it "comes from" $3-x=\sqrt{15-x}$ or from $3-x=-\sqrt{15-x}\;$? It can't. So it has to play it safe and give you all the solutions of $3-x=\sqrt{15-x}$, and also all the solutions of $3-x=-\sqrt{15-x}$.

And, as you can readily check, the extraneous solution that you got is indeed the solution of the equation $3-x=-\sqrt{15-x}$.

Geometric interpretation: The curve $y=\sqrt{15-x}$ is half of a parabola. When you square both sides of $y=\sqrt{x-5}$, you get $y^2=x-5$, which is the full parabola. So when you squared both sides, the algebra decided that you wanted the intersection points of the line with the full parabola. And that's exactly what the algebra produced. By looking at the original picture, and the two candidates for solution, you can tell instantly which one is not valid.

André Nicolas
  • 507,029
2

When you square both sides, you often introduce extraneous solutions. Squaring is a non-reversible operation, which is why you create them. In your case, plugging $6$ in to the left gives $3-6=-3$, while plugging it in to the right gives $\sqrt{15-6}=3$. As $(-3)^2=3^2$, this "solution" appears.

Ross Millikan
  • 374,822
  • So it is a must to add a step to the solution above to eliminate the extraneous solution. – NoChance Oct 04 '11 at 00:47
  • @EmmadKareem: Exactly. The solutions you found are candidate solutions. All the real solutions will be within the ones you found, but you need to check them back in the original equation to find which are real and which are extraneous. If every step in your solution is reversible, you don't need to check. You have proved that $3-x=\sqrt{15-x} \implies x \in {-1,6}$ but not that $x \in {-1,6} \implies 3-x=\sqrt{15-x}$ – Ross Millikan Oct 04 '11 at 04:30