complex numbers - argand diagram

Question

How do you draw on an argand diagram: $\{z\in{\mathbb C}: \arg(z-1) < \arg(z-i)\}$?
I can plot both points but I don't know what to do with arguments and inequalities.

Answer 1

If you simply interpret what it means to say that $\arg(z-1)<\arg(z-i)$ geometrically, then it shouldn't be too hard to visualize the region. In each of the regions below, the argument of the point ($z$) minus the number (either $1$ or $i$) simply the angle from the dashed line to the arrow. It's easy to see that this angle is smaller from the complex number $1$ in exactly the blue regions.

Note that I'm assuming a branch cut at $\pi$ in the argument function so that, in the horizontal strip, $\arg(z-1)$ is definitely negative while $\arg(z-i)$ is positive.

Answer 2

Setting $\displaystyle z=x+iy,$ we need $$\arctan\frac y{x-1}<\arctan\frac{y-1}x$$

$$\iff\arctan\frac y{x-1}-\arctan\frac{y-1}x<0 $$

$$\iff\arctan\left(\frac{\dfrac y{x-1}-\dfrac{y-1}x}{1+\dfrac y{x-1}\cdot\dfrac{y-1}x}\right)<0 $$

$$\iff\arctan\left(\frac{x+y-1}{x^2+y^2-x-y}\right)<0 $$

$$\iff\frac{x+y-1}{x^2+y^2-x-y}<0 $$

So, we need the sign of $\displaystyle x+y-1$ and $\displaystyle x^2+y^2-x-y=\left(x-\frac12\right)^2+\left(y-\frac12\right)^2-\frac12$ to be opposite

We know, $\displaystyle \left(x-\frac12\right)^2+\left(y-\frac12\right)^2-\frac12=0$ is a circle with radius $\frac1{\sqrt2}$ with center at $\left(\frac12,\frac12\right)$.

Edit

As can easily be plotted on WolframAlpha, this region looks like so:

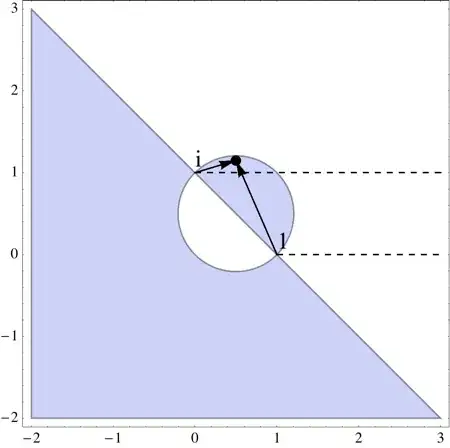
Unfortunately, the arguments can easily be read off of the image as the angles between the vectors and the dashed lines. It certainly appears that $\arg(z-1)>\arg(z-i)$ for certain points in the region.