Title says it all. And the one that I know is below. (image from wikipedia)
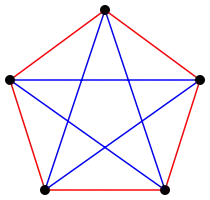
My question is: Is there only one counter example in $K_5$ for $R(3,3)$ where $K_5$ is a complete graph of 5 points and $R(s,t)$ is Ramsey number.
Title says it all. And the one that I know is below. (image from wikipedia)

My question is: Is there only one counter example in $K_5$ for $R(3,3)$ where $K_5$ is a complete graph of 5 points and $R(s,t)$ is Ramsey number.
Yes, try it yourself. If you start out with one node connected to 3 or 4 edges of the same colour, you will find it impossible to complete the graph.
Hence every node must be connected to two red and two blue edges. Starting with this, and keeping this rule for every node, you are forced to end up with the coloring of $K_5$ you've shown. You'll notice you will have a choice for one edge, but both will lead to either the coloring you've shown or one that looks different, but is in fact isomorphic to the one you've shown (two nodes have just moved around).
Another way to think about it: How many graphs $G$ are there on 5 vertices such that both $G$ and $\overline{G}$ are triangle free?
$C_5\cong\overline{C_5}$ is the only answer.
This coloring has the property that
each vertex is incident to exactly two red edges and two blue edges. (Property $X$)
Any $R(3,3)$ coloring of $K_5$ must have this property. For suppose we had an $R(3,3)$ coloring of $K_5$ that did not have property $X$. Then there is some vertex $v$ with at least three edges of the same color, say red. These three edges are also incident to vertices $u_1, u_2, u_3$. Each edge $u_i-u_j$ must be blue, or else $v, u_i, u_j$ would be vertices of a red triangle. But then $u_1, u_2, u_3$ are vertices a blue triangle. So any $R(3,3)$ coloring must have property $X$.
Now consider the subgraph consisting of just the red edges. Every vertex in this subgraph has degree 2. It is an easy theorem that such a graph is a union of disjoint cycles. In this case, there can't more than one cycle because that would require at least 6 vertices and we have only 5. So the red edges must form a single cycle of length 5. We can then arrange the vertices so that this cycle is the outer pentagon, as you did, and then the blue edges must be the inner pentagram, also a cycle of length 5.