Are there any explanations for these patterns in the Collatz sequences?

Question

I've been messing around with the Collatz sequences a bit, and have come across a few patterns - I was wondering if there are any known explanations for these patterns.

The first is the plot of stopping times (sequence lengths) for all Collatz sequences beginning with the first $100,000$ integers. As confirmed by both the wikipedia page and by this quick Python script/Excel plot, this strange line-pattern exists in the stopping times:

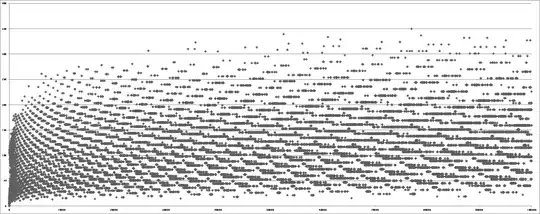
Another pattern was in the number of "hits" for each number. By that, I mean the number of unique sequences a specific number exists in. Generated by this similar Python script, its showing very strange patterns (if anyone wants the excel file generated, its here- just make sure you don't select the ads that look like download buttons). Specifically, one of the patterns I immediately noticed was this counting patterns - every third integer has a countdown number of hits. For example, here are the first 20 integers:

$$ \begin{array}{c|c} 1 &0 \\ 2 &99998 \\ 3 &16 \\ 4 &99997 \\ 5 &93742 \\ 6 &15 \\ 7 &19146 \\ 8 &99996 \\ 9 &14 \\ 10 &93741 \\ 11 &44375 \\ 12 &14 \\ 13 &47646 \\ 14 &19145 \\ 15 &13 \\ 16 &99995 \\ 17 &46031 \\ 18 &13 \\ 19 &17685 \\ 20 &93724 \\ \end{array} $$

Notice how everything else looks random, but every third integer counts down. This pattern remains throughout the whole of the $100,000$ integers (though the spaces between each different number in the countdown increase dramatically).

If anyone knows an explanation for these patterns, or can direct me towards further reading about these patterns, it'd be grealy appreciated.

Answer 1

Hmm, I'm not sure that I got you right. But it seems to me, that this is simply a consequence of any tree-structure, that there are numbers near the root through which many pathes go and that there are other numbers, far away from the root, through which less pathes go. And now, the Collatz-transformation-rule can be written in an inverted tree, say $$ \begin{array}{} & 1 \to 2 & \to 4 & \to 8 &\to 16 &\to 32 &\to \cdots\\ & & & & \to 5 &\to 10 & \to 20 & \to 40 & \to \cdots\\ & & & & & & & \to 13 & \to 26 & \to \cdots\\ & & & & & \to 3 & \to 6 & \to 12 &\to \cdots\\ \end{array} $$ or much better visible in this (very old) link then it is obvious that the number $2$ is "on the path" of many transformations, and $3$ or $13$ much less - where "many" and "less" is a bit sloppy for comparisions of infinite numbers, but it may be taken as more or less when the numbers are only taken by some finite subset.
The graphs in my link might be a bit difficult to read - I just left out the even numbers because... well, they might be seen as "trivial" and ... they didn't complain ;-)

Answer 2

Counting Down

The reason the number of hits for each number of the form $3\times2^n$ declines by one for every increment of $n$, is that there are no branches leading to any multiple of $3$, only a single path containing $3\times 2^n\mid n\in\mathbb{N}$.

Therefore every next highest element of this set has exactly one fewer predecessors in any given range. of course they all have infinitely many if you extend your range through all the integers.

Stopping Times

This is a bit less clear to understand but basically the structure is built by the intersection between the functions $x\to x/2$ and $x\to 3x+1$. You can see the dots clustered in two curves, one with a positive gradient and the other with a negative.

If we imagine any sequence represented by a series of zeroes and ones depending which function is applied and in which order, and we imagine starting from $1$ and working in reverse, then the clusters of close horizontal points occur where there is one less application of one function, and one more of the other, and these are exchanged in such a pair of positions that the overall effect upon the final integer is at its least. For any given integers there is a pair or more of digits in the binary string which can be changed to have minimal effect upon the final number.

Answer 3

The “strange line patterns” are a consequence for the several consecutive numbers with the same total stopping time, which I suspect is due to the limitations posed by the odd rule 3x+1. As for the every third number counting down, the other commentators explained the use of a sample size: in this case the first 100,000 positive integers, is to blame.

I am a math amateur, my personal ideas and work about the total stopping times are most likely naive at best. However, I came across this research paper that analyzed consecutive values and their properties:

https://web.math.rochester.edu/people/faculty/abeeson/Elia_Tucker.pdf

The counting down pattern made by every third integer is a consequence of having a sample size to begin with, regardless of the size of the sample. If you only did the first 10 numbers instead of the first 10,000 numbers, 3 would still have the larger value of 2 compared to 6 and 9 which would both have a value of 1. As the sample size gets bigger, the smaller multiples of 3 will get the larger numbers just for showing up more often in 3x+1 sequences.

Answer 4

3n+1 obviously cannot take us onto an even number divisible by 3, so what the 3(16), 6(15), 9(14) etc part of the list suggests to me is that these numbers can only feature in sequences at the beginning section of the sequence (eg 12 halves to 6 halves to 3 then goes by 3n+1 to 10 then halving to 5 etc....).

My guess - that's all it is - is that when you count all the sequences starting with a given multiple of 3 and take into account double-counting you get this ranking. Obviously the larger the multiple of 3, the fewer sequences will involve it, and there is clearly something going on with odd multiples of 3, and the instances of double or quadruple that multiple.

For example if 16 sequences start with or involve a 3, it doesn't seem odd that 15 sequences start with or involve a 6 (all 15 of them will immediately have 3 as the member right after 6, and there is only one sequence that can start with a 3, so that's the 16th in the list next to "3").

Answer 5

Number 3 you will never find, after you go just a little away from the start (of counting hits) and there is a way to prove it (I can not prove, because I am not good with proofs, by a professor proved it once for me). That is the reason 6 only show a few times, because it is 3*2.

The same logic applies every 3 numbers, because they are divided by 3, and this won't show it anymore, once it gets on even function, they will go to the odd function and it will never have an ouput with 3 as factor ever again from that on.

I guess it just goes with the fact, that when you get a number on odd function, it goes 3n+1 and then is never divisible from 3. You only need to prove that. And that is your question.

Sorry for not having a definite answer, as why is this.

If you want a pattern to work on: take a look at one I found it about collatz. Collatz Pattern