Show that the sequence $a_{n+1}=a_{n}+\dfrac{a^2_{n}}{n^2}$ is upper bounded

Question

Let $\{a_{n}\}$ be defined with $a_{1}\in(0,1)$, and $$a_{n+1}=a_{n}+\dfrac{a^2_{n}}{n^2}$$ for all $n\gt 0$. Show that the sequence is upper bounded.

My idea: since $$a_{n+1}=a_{n}\left(1+\dfrac{a_{n}}{n^2}\right)$$ then $$\dfrac{1}{a_{n+1}}=\dfrac{1}{a_{n}}-\dfrac{1}{a_{n}+n^2}$$ then $$\dfrac{1}{a_{n}}-\dfrac{1}{a_{n+1}}=\dfrac{1}{a_{n}+n^2}$$ so $$\dfrac{1}{a_{1}}-\dfrac{1}{a_{n+1}}=\sum_{i=1}^{n}\dfrac{1}{a_{i}+i^2}$$ since $$a_{n+1}>a_{n}\Longrightarrow \dfrac{1}{a_{i}+i^2}<\dfrac{1}{a_{1}+i^2}$$ so $$\dfrac{1}{a_{n+1}}>\dfrac{1}{a_{1}}-\left(\dfrac{1}{1+a_{1}}+\dfrac{1}{2^2+a_{1}}+\cdots+\dfrac{1}{a_{1}+n^2}\right)$$ But the RHS might be $\lt0$ for a sufficiently large starting value; for instance, with $a_{1}=\dfrac{99}{100}$ then $$\dfrac{1}{a_{1}}-\left(\dfrac{1}{1+a_{1}}+\dfrac{1}{2^2+a_{1}}+\cdots+\dfrac{1}{a_{1}+n^2}\right)<0,n\to\infty$$

see:

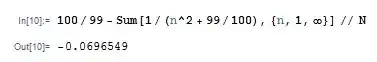
so this method won't let me bound the series and I don't know what else to do.

Answer 1

Here is a solution: Since $(a_{n})$ is monotone increasing, either it remains bounded or it diverges to $+\infty$. Assume that $a_{n} \nearrow +\infty$.

Observation 1. Referring to OP's identity

$$ \frac{1}{a_{n}} - \frac{1}{a_{n+1}} = \frac{1}{a_{n} + n^{2}}, $$

we have

$$ \frac{1}{a_{n}} - \frac{1}{a_{m+1}} = \sum_{k=n}^{m} \frac{1}{a_{k} + k^{2}}. $$

Taking $m \to \infty$, it follows that

\begin{align*} \frac{1}{a_{n}} = \sum_{k=n}^{\infty} \frac{1}{a_{k} + k^{2}} \leq \sum_{k=n}^{\infty} \frac{1}{k^{2} - k} = \frac{1}{n-1}. \end{align*}

Thus we must have $n-1 \leq a_{n}$ for any $n \geq 2$.

Observation 2. Now we prove that $a_{n} \leq a_{1} n$ for any $n$. Indeed, this is trivial when $n = 1$. Also, if it holds for $n$ then

$$ a_{n+1} = a_{n} \left( 1 + \frac{a_{n}}{n^{2}} \right) \leq n a_{1} \left( 1 + \frac{1}{n} \right) = (n+1)a_{1}. $$

Therefore by induction, we have the desired estimate.

Conclusion. Combining two observation, it follows that

$$n - 1 \leq a_{n} \leq na_{1} \quad \Longrightarrow \quad 1 - \frac{1}{n} \leq a_{1}.$$

for $n \geq 2$. Taking $n\to\infty$, we have $1 \leq a_{1}$, a contradiction! Therefore $(a_{n})$ must remain bounded.

---

Addendum. Now let us investigate an asymptotic behavior of the limit $f(a_{1}) = \lim_{n\to\infty} a_{n}$. We have

\begin{align*} \frac{1}{a_{1}} - \frac{1}{f(a_{1})} &= \sum_{n=1}^{\infty} \frac{1}{n^{2} + a_{n}} \geq \sum_{n=1}^{\infty} \frac{1}{n^{2} + n} = 1, \end{align*}

So we have a lower bound.

$$ f(a_{1}) \geq \frac{a_{1}}{1 - a_{1}}. $$

Answer 2

Now,today I have solve this problem,I post my methods,I hope is not wrong?

since $$a_{n+1}=a_{n}\left(1+\dfrac{a_{n}}{n^2}\right)$$ then $$\dfrac{1}{a_{n+1}}=\dfrac{1}{a_{n}}-\dfrac{1}{a_{n}+n^2}$$ then $$\dfrac{1}{a_{n}}-\dfrac{1}{a_{n+1}}=\dfrac{1}{a_{n}+n^2}$$ so $$\dfrac{1}{a_{1}}-\dfrac{1}{a_{n+1}}=\sum_{i=1}^{n}\dfrac{1}{a_{i}+i^2}$$ so $$\dfrac{1}{a_{n+1}}=\dfrac{1}{a_{1}}-\left(\dfrac{1}{a_{1}+1^2} +\dfrac{1}{a_{2}+2^2}+\cdots+\dfrac{1}{a_{n}+n^2}\right)$$ by induction,we have $$a_{n}>nt^{n+1},t=\sqrt{a_{1}}\in (0,1)$$ because $$a_{n+1}=a_{n}+\dfrac{a^2_{n}}{n^2}>nt^{n+1}+t^{2n+2}$$ we only prove $$nt^{n+1}+t^{2n+2}>(n+1)t^{n+2},t=\sqrt{a_{1}}\in (0,1)$$ $$\Longleftrightarrow n+t^{n+1}-(n+1)t>0$$ use this Bernoulli inequality: $$(1+x)^n\ge 1+nx,x>-1,n>1$$ then we have $$t^{n+1}=(1+t-1)^{n+1}>1+(n+1)(t-1)=1+(n+1)t-(n+1)$$ Now $$\dfrac{1}{a_{n+1}}>\dfrac{1}{t^2}-\left(\dfrac{1}{t^2+1}+\dfrac{1}{2t^3+2^2}+\cdots+\dfrac{1}{nt^{n+1}+n^2}\right)$$ other hand,Use AM-GM inequality,we have \begin{align*} \dfrac{1}{t^2+1}+\dfrac{1}{2t^3+2^2}+\cdots+\dfrac{1}{nt^{n+1}+n^2}&=\dfrac{1}{1(1+t^2)}+\dfrac{1}{2(1+1+t^3)}+\cdots+\dfrac{1}{n(1+1+\cdots+1+t^{n+1})}\\ &<\dfrac{1}{2t}+\dfrac{1}{2\times 3t}+\cdots+\dfrac{1}{n(n+1)t}\\ &=\dfrac{1}{t}\left(1-\dfrac{1}{n+1}\right)\\ &<\dfrac{1}{t} \end{align*} so $$\dfrac{1}{a_{n+1}}>\dfrac{1}{t^2}-\dfrac{1}{t}$$ $$\Longrightarrow a_{n+1}<\dfrac{t^2}{1-t}$$

Answer 3

We have $$\frac{a_{n+1}}{a_n} = 1 + \frac{a_n}{n^2}$$

Therefore, if the product $$\prod_{n=1}^{\infty} ( 1+ \frac{a_n}{n^2})$$ is bounded, then so is $a_n$. Since $1+x \le e^x$, it is enough to show that $\sum_{n\ge 0} \frac{a_n}{n^2} < \infty$. Now, this would follow from $\frac{a_n}{n} < n^{1-\epsilon}$ for some $\epsilon>0$.

Now, for the sequence $b_n\colon = \frac{a_n}{n}$ we have $$b_{n+1} = \frac{n b_n + b_n^2}{n+1}$$ so by induction $1 > b=b_1 > b_2 > \ldots > 0$. Now we have $$\frac{b_{n+1}}{b_n} = \frac{1+ \frac{b_n}{n} }{1 + \frac{1}{n}}$$

Now, the partial products of the infinite product $$\prod_{n=1}^{\infty} \frac{1 + \frac{b}{n}}{1 + \frac{1}{n}}$$ decrease like $n^{b-1}$. We are done.

$\bf{Added:}$ A similar argument shows that the sequence of holomorphic function $\phi_1(z) =z$, $\phi_{n+1}(z) = \phi_n(z) + (\frac{\phi_n(z)}{n})^2$, converges uniformly on compacts to a holomorphic function $\phi(z)$ on the unit disk $D(0, 1)$.

Answer 4

When the exponent is $\alpha,\alpha \gt 1$, the proof is as follows. $$ \frac{a_{n+1}-a_{n}}{a_n^\alpha}=\frac{1}{n^{\alpha}}\\ $$ then $\sum_{n=M}^\infty\frac{a_{n+1}-a_{n}}{a_n^\alpha}$ converges. Let $T_N=\sum_{n=M}^N\frac{a_{n+1}-a_{n}}{a_n^\alpha}, N\ge M,T_N$ is monotonically increasing. $$\begin{align} T_N&=\sum_{n=M}^N\int_{a_n}^{a_{n+1}}\frac{dx}{a_n^\alpha}\\&\gt\sum_{n=M}^N\int_{a_n}^{a_{n+1}}\frac{dx}{x^\alpha}\\&=\frac{1}{1-\alpha}(a_{N+1}^{1-\alpha}-a_{M}^{1-\alpha})\\ T_N&=\sum_{n=M}^N\frac{1}{n^{\alpha}}\\&\lt\sum_{n=M}^{\infty}\frac{1}{n^{\alpha}}\\&=\frac{1}{M^{\alpha}}+\sum_{n=M+1}^{\infty}\frac{1}{n^{\alpha}}\\&\lt\frac{1}{M^{\alpha}}+\sum_{n=M+1}^{\infty}\int_{n-1}^n\frac{dx}{x^{\alpha}}\\&=\frac{1}{M^{\alpha}}+\frac{M^{1-\alpha}}{\alpha-1}\end{align} $$ there is an inequality: $$ \frac{1}{1-\alpha}(a_{N+1}^{1-\alpha}-a_{M}^{1-\alpha})\lt\frac{1}{M^{\alpha}}+\frac{M^{1-\alpha}}{\alpha-1}\\ \Rightarrow a_{N+1}^{1-\alpha}\gt a_{M}^{1-\alpha}-(\alpha-1)M^{-\alpha}-M^{1-\alpha} $$ we need to show $a_{M}^{1-\alpha}-(\alpha-1)M^{-\alpha}-M^{1-\alpha}\gt 0$. Notes $a_n\lt na_1$, then $$ (Ma_1)^{1-\alpha}\lt a_M^{1-\alpha}\\ \Rightarrow a_{M}^{1-\alpha}-(\alpha-1)M^{-\alpha}-M^{1-\alpha}\gt (Ma_1)^{1-\alpha}-(\alpha-1)M^{-\alpha}-M^{1-\alpha}\\\gt 0 $$ Iff $$ M\gt \frac{\alpha-1}{a_1^{1-\alpha}-1} $$