Why $\sum\limits_{i=1}^n \frac{1}{i} =\mathcal O(\ln(n))$?

Question

I am reading textbook proof on algorithms that uses this fact:

$$\sum_{i=1}^n \frac{1}{i} =\mathcal O(\ln(n)).$$

Why is that true? I'm trying to use Taylor series to find out why, but I'm not making much progress.

Answer 1

For every nonincreasing function $u$ and every $k$, $$ \int_{k}^{k+1}u(x)\,\mathrm dx\leqslant u(k)\leqslant \int_{k-1}^ku(x)\,\mathrm dx, $$ hence $$ \int_1^{n+1}u(x)\,\mathrm dx\leqslant\sum_{k=1}^nu(k)\leqslant u(1)+\int_1^nu(x)\,\mathrm dx. $$ If $u:x\mapsto1/x$, the RHS is $1+\log n$ and the LHS is $\log(n+1)$ hence, for every $n\geqslant1$, $$ \log n\leqslant\sum_{k=1}^n\frac1k\leqslant1+\log n. $$ The sum in the middle is called $H_n$ the $n$th harmonic number and one knows that, when $n\to\infty$, $H_n-\log n\to\gamma$ the Euler constant, with $\gamma\approx0.577$.

Answer 2

Using Taylor series is working too hard! Recall the definition of $\ln$ (or, at least, a property): $$\ln(x) = \int_1^x \frac 1xdx$$ If $x \in \Bbb N$, we also have from the definition of the integral $$\int_1^x \frac 1x dx \geq \sum_{n=2}^x \frac 1n$$

You can see that pictorially here (picture stolen from Paul's Online Math Notes):

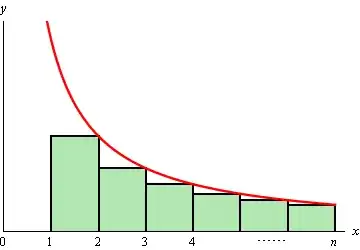
We also have $\sum_{n=2}^x \frac 3n \geq \sum_{n=1}^x \frac 1n$ for $n \in \Bbb N$ (which you can prove by induction or otherwise), so that $$3\ln(x) \geq \sum_{n=1}^x \frac 1n$$ and thus $\sum_{n=1}^x \frac 1n = O(\ln(x))$ as desired.