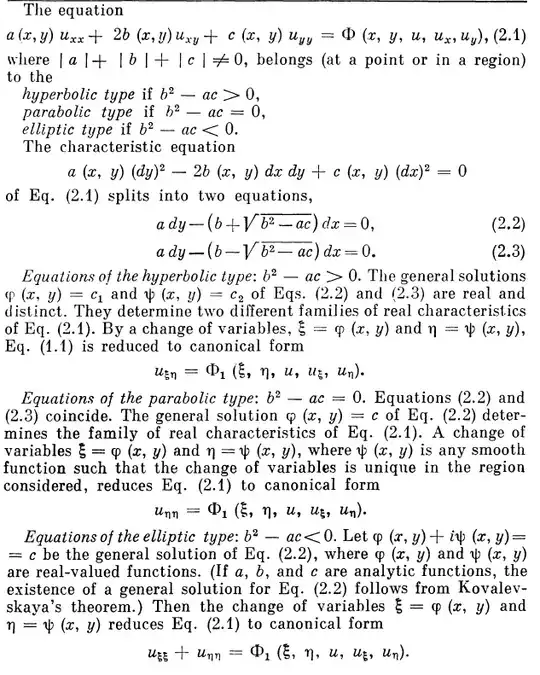Can anyone help me find the canonical form of
$$x^2u_{xy} - yu_{yy} + u_x - 4u = 0?$$
I don't know how to solve it because $a = 0$. I just got that it's hyperbolic since $a=0$ , $b =(x^2)/2$, $c= -y$, then we have $b^2- ac =\frac{x^4}4-0=\frac{x^4}4 > 0$ (hyperbolic), where $x \neq 0$.
see: V.S.Vladimirov, A Collection of Problems on the Equations of Mathematical Physics, Springer, 1986
In your case characteristic equation is $$-x^2dxdy-ydx^2=0$$ with solutions $$x=c_1,\quad -1/x+\log(y)=c_2.$$ By a change of variables $$\xi=x,\quad\eta=-1/x+\log(y)$$ we get canonical form $$u_{\xi\eta}=\frac{{{e}^{\frac{1}{\xi }+\eta }}\, \left( {{\xi }^{2}}\, {u_{\xi }}-4 u\, {{\xi }^{2}}+{u_{\eta }}\right) }{{{\xi }^{4}}}-\frac{{u_{\eta }}}{{{\xi }^{2}}}$$
