2

OK,

I need the integral of

$$ f(x,y)=e^{-\beta\left(x^{2}+y^{2}\right)} $$

(beta is a constant)

over this green region, where we integrate from the origin outwards.

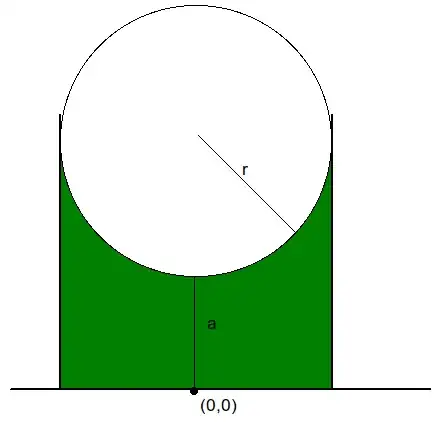
enter image description here

Any help? I tried in Tricky Gaussian; a good method?, but to no avail.

Community
  • 1
apg
  • 2,797

1 Answers1

1

I don't think this can be evaluated explicitly. The integral is easy enough to set up:

$$\int_{-r}^r dx \, e^{-\beta x^2} \, \int_0^{a+r-\sqrt{r^2-x^2}} dy \, e^{-\beta y^2}$$

which may be expressed as a single integral:

$$\frac12 \sqrt{\frac{\pi}{\beta}} \int_{-r}^r dx \, e^{-\beta x^2} \operatorname*{erf}{\left [ \sqrt{\beta} \left ( a+r-\sqrt{r^2-x^2}\right )\right ]}$$

You can do a sub $x=r \cos{\theta}$, but it is unclear to me how this results in anything more useful.

Ron Gordon
  • 138,521
  • 1
    I have got this far. Comment on this: If I sub u=x/r, getting an integral between 0 and 1 (if I cut things in half), is it possible to approximate the integral by expanding the integrand at 0 (which might be accurate enough between the limits)? Of course this is possible, but will it be accurate enough to be considered a good approximation? Hmmm... – apg Feb 14 '14 at 01:12
  • 1
    Maybe have a look at http://math.stackexchange.com/questions/78615/integrating-a-product-of-exponentials-and-error-functions?rq=1, it might help, though arranging things such that we can make things simpler this way seems non-trivial... – apg Feb 14 '14 at 01:17
  • @AlexanderGiles: you could, but my gut tells me that this is not going to get you very much accuracy for the effort. I would just do a simple numerical quadrature, as erf and the gaussian make for a simple, smooth function. – Ron Gordon Feb 14 '14 at 01:19
  • 1
    can't use numerical intergration - need a result or approximation for small a. – apg Feb 14 '14 at 01:39
  • 1
    Perhaps the second answer in http://math.stackexchange.com/questions/78615/integrating-a-product-of-exponentials-and-error-functions?rq=1 could help? – apg Feb 14 '14 at 15:53