2

I am trying to work out if the centre of rotation of a measured sphere is actually at 0,0 or slightly offset from the centre.

The situation is as follows: I have a machine tool with a table that rotates about its centre. I wish to verify that the centre of the table is at 0,0 according to the machine coordinate system. I have measured the centre position of a sphere mounted on the table at various rotations of the table so have a number of x,y coordinates for the sphere centre relative to 0,0 (note: the sphere was not necessarily mounted on the table at x=0). Hopefully the image helps to illustrate this.

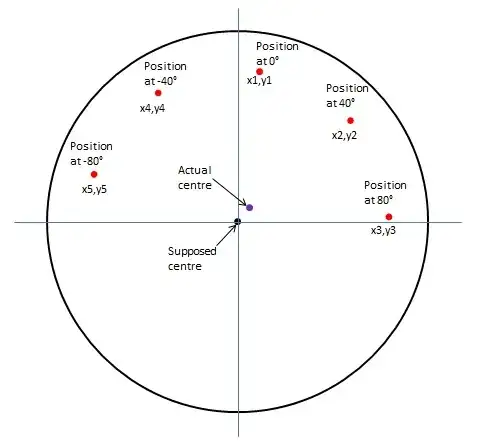
centre of rotation

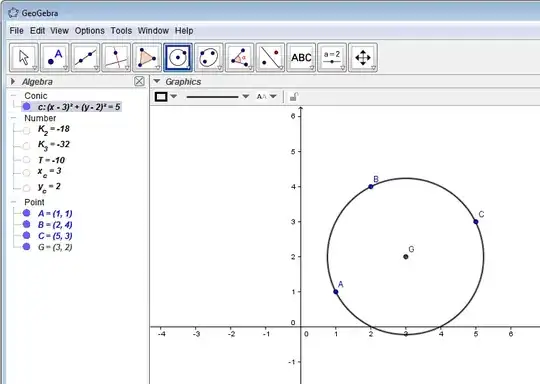
I would like to be able to calculate the actual centre of rotation (shown by the purple dot) from these coordinates and the angles.

I have a feeling that there is a simple way of doing this but I cannot work it out.

Any help on this would be greatly appreciated.

Many thanks in advance.

guitarmanjon
  • 21

3 Answers3

1

This is a problem of circular regression. The answer is in : https://fr.scribd.com/doc/14819165/Regressions-coniques-quadriques-circulaire-spherique

Since this paper is written in French, I joint a copy of the equations to be used :

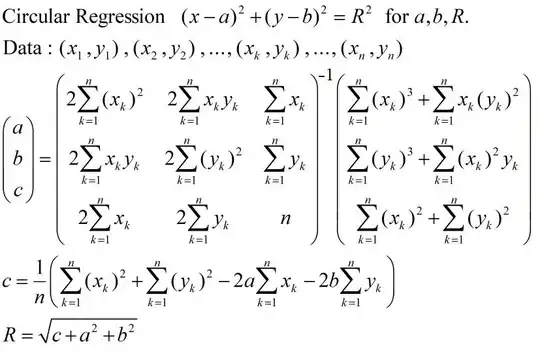
enter image description here

The radius ($R$) is the radius of the circle fitted to the set of points.

Same method, matrix presentation :

enter image description here

JJacquelin
  • 66,221
  • 3
  • 37
  • 87
1

You just need three measurements, say $P_i=(x_i,y_i)$ for $i=1,2,3$.

Let $L_1$ be the perpendicular bisector of $P_1 P_2$ and $L_2$ be the perpendicular bisector of $P_2 P_3$.

The centre is the point where $L_1$ and $L_2$ intersect.

Amritanshu Prasad
  • 1,784
  • Great, thanks for the response. Any ideas how I would calculate the point where L1 and L2 intersect? I know I can do it by drawing it but I would like to be able to include it in the program for the machine. Thanks again. – guitarmanjon Feb 13 '14 at 16:08
  • You should be able to write out the equations of these lines. For example, slope of $L_1$ is the negative reciprocal of the slope of $P_1P_2$ and it passes through the midpoint $(\frac{x_1+x_2}2,\frac{y_1+y_2}2)$. Once you have these equations $y = m_1x+c_1$ and $y=m_2x+c_2$, find the intersection point by solveing $m_1x +c_1=m_2x+c_2$. – Amritanshu Prasad Feb 13 '14 at 16:46
  • Thank you once again. I will approach it as you suggest. Clearly my high school maths hasn't been used enough over the last few years! – guitarmanjon Feb 14 '14 at 09:44
  • It's a nice problem. Can I use it in a magazine column that I edit? How can I acknowledge you? – Amritanshu Prasad Feb 14 '14 at 10:26
  • Yes, of course.

    My name is Dr. Jon Stammers and I work at the "AMRC with Boeing". Please let me know if you need any more information.

     – guitarmanjon Feb 14 '14 at 10:42
  • It's called "Problems and Solutions" in the Mathematics Newsletter of the Ramanujan Mathematical Society. If you send me e-mail address (mine can be found at http://www.imsc.res.in/~amri/, I can get in touch with you). – Amritanshu Prasad Feb 14 '14 at 11:40
  • I know this is old, but this method doesn't work if P1 and P2 are co-linear with the center point. – Gorchestopher H Mar 09 '23 at 20:11
0

For each three points you can find the circle that passes through those points. Mark the center of this circle. Repeat for all the combinations of three points and average the resulting x and y coordinates of the circle.

Look at https://math.stackexchange.com/a/213670/3301 for one of the ways you can get the circle center from three points.

The generelized version of this method is to calculate the following parameters from the coordinates $(x_1,y_1)$, $(x_2,y_2)$ and $(x_3,y_3)$

$$ T = x_1 (y_2-y_3)+x_2 (y_3-y_1) + x_3 (y_1-y_2) $$ $$ K_2 = (x_1^2-x_2^2)+(y_1^2-y_2^2) $$ $$ K_3 = (x_1^2-x_3^2)+(y_1^2-y_3^2) $$

Now the circle center is located at

$$ x_c = \frac{K_2 (y_1-y_3)+K_3 (y_2-y_1)}{2 T} $$ $$ y_c = -\frac{K_2 (x_1-x_3)+K_3 (x_2-x_1)}{2 T} $$

With the example provided in the link you get (3,2) for the center

Geo

Community
  • 1
John Alexiou
  • 13,816