A colleague of mine came across this equation on an old exam: $$ \int_0^{\pi}{\cos n\theta\over\cos\theta-\cos\phi}\,d\theta={\pi\sin n\phi\over\sin\phi} $$ It said on the exam that students were allowed to assume this result.
My colleague (and I) would be much obliged if someone could present a reference to, or a proof of (or a refutation of), this formula. I suppose one is to assume $n$ is a positive integer.
I am going to attack this problem here because a) this was never closed as a duplicate, and b) the link given in the comments above is to an alleged duplicate in which the accepted answer is useless enough to be not even wrong. I will demonstrate.
Consider the following contour integral:
$$ \oint_C \frac{dz}{z^n} \frac{z^{2 n}+1}{z^2-2 z \cos{\phi}+1} $$
where $C$ is the following contour:
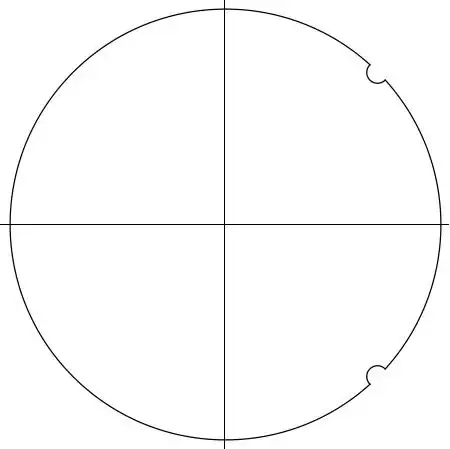
$C$ is the positively-oriented unit circle deformed at $z=e^{\pm i \phi}$ by semicircles of radii $\epsilon$ into the unit circle. Thus, the only pole of the integrand is at $z=0$.
The contour integral is thus equal to
$$i \int_{-\pi}^{-\phi-\epsilon} d\theta \frac{\cos{n \theta}}{\cos{\theta}-\cos{\phi}} + i \epsilon \int_{\pi}^0 dt \, e^{i t} \frac{(e^{-i \phi}+\epsilon e^{i t})^n + (e^{-i \phi}+\epsilon e^{i t})^{-n}}{(e^{-i \phi}+\epsilon e^{i t})^2-2 \cos{\phi} (e^{-i \phi}+\epsilon e^{i t})+1} \\ +i \int_{-\phi+\epsilon}^{\phi-\epsilon} d\theta \frac{\cos{n \theta}}{\cos{\theta}-\cos{\phi}} + i \epsilon \int_{\pi}^0 dt \, e^{i t} \frac{(e^{i \phi}+\epsilon e^{i t})^n + (e^{i \phi}+\epsilon e^{i t})^{-n}}{(e^{i \phi}+\epsilon e^{i t})^2-2 \cos{\phi} (e^{i \phi}+\epsilon e^{i t})+1}\\ +i \int_{\phi+\epsilon}^{\pi} d\theta \frac{\cos{n \theta}}{\cos{\theta}-\cos{\phi}}$$
We now take the limit as $\epsilon \to 0$. In this limit, the second integral and the fourth integrals cancel each other out because they approach the value
$$\frac{\pi \cos{n \phi}}{\sin{\phi}} - \frac{\pi \cos{n \phi}}{\sin{\phi}} $$
The contour integral is also equal to $i 2 \pi$ times the residue of the pole $z=0$. Thus, we have
$$i PV \int_{-\pi}^{\pi} d\theta \frac{\cos{n \theta}}{\cos{\theta}-\cos{\phi}} = \frac{i 2 \pi}{(n-1)!} \left [ \frac{d^{n-1}}{dz^{n-1}} \frac{z^{2 n}+1}{z^2-2 z \cos{\phi}+1} \right ]_{z=0} $$
As for the term in the brackets, we note that the $(n-1)$th derivative of a product of two functions is simply a binomial-type expression:
$$\frac{d^{n-1}[f(z) g(z)]}{dz^{n-1}} = \sum_{k=1}^{n-1} \binom{n-1}{k} \frac{d^k f(z)}{dz^k} \frac{d^{n-1-k} g(z)}{dz^{n-1-k}} $$
where $f(z) = z^{2 n}+1$ and $g(z)=(z^2-2 \cos{\phi}+1)^{-1} $. Note that, because we are evaluating this derivative at $z=0$, all derivative terms involving $f(z)$ are zero. Since $f(0)=1$, our residue is merely
$$\frac1{(n-1)!} \left [ \frac{d^{n-1}}{dz^{n-1}} \frac{1}{z^2-2 z \cos{\phi}+1} \right ]_{z=0} $$
At this point I invoke the well known generating function for the Chebyshev polynomial of the second kind is
$$\frac1{z^2-2 x z+1} = \sum_{k=0}^{\infty} U_k(x) z^k $$
where
$$U_k(\cos{\phi}) = \frac{\sin{(k+1) \phi}}{\sin{\phi}} $$
Thus, we may finally say that
$$PV \int_{-\pi}^{\pi} d\theta \frac{\cos{n \theta}}{\cos{\theta}-\cos{\phi}} = 2 \pi \frac{\sin{n \phi}}{\sin{\phi}}$$
and the stated result follows.
I may now explain my "not even wrong" comment above. If one follows the hint given in the accepted answer in the above-linked-to question, one may arrive at this correct answer. However, that hint is terrible advice based on a fundamental misunderstanding of contour integration techniques. Integrals of functions having poles on the contour are undefined unless defined in a Cauchy principal value sense, as done above. (Note here that by "PV", I mean avoiding both poles.) It just so happened that the contributions of the deformed pieces of the contour cancel; most times, that will certainly not be the case. That's why the hint is not even wrong: because, by taking it, one stumbles upon the correct result without appreciating why.