Please help me find the summation of following series under limit.
$$ \lim_{n \to \infty} \sum_{x = 1}^{n}{1 \over x}\,\cos\left(\left[x - 1\right]{\pi \over 3}\right) $$
Thank you. :)
Asked
Active
Viewed 144 times
2 Answers
5
Hint: The $\cos$ terms form a pattern for each six terms: $1, 1/2, -1/2, -1, -1/2, 1/2,$ and back to $1$. That would at least let you split the series up into ones that are more manageable.
John
- 26,319
-
Well,it does look like it may help the case but still I am unable to use it. The difficulty is arising because the sum is made up of product of two different type of progressions! So, if you can kindly provide a solution then it would be of greater help. Thank you! :) – Abir Mukherjee Feb 10 '14 at 18:11
5
Your sum is the real part of $$ e^{-i\pi/3}\sum_{k=1}^\infty\frac1ke^{ik\pi/3} $$ which is the series for $$ \begin{align} -e^{-i\pi/3}\log\left(1-e^{i\pi/3}\right) &=-\left(\frac12-i\frac{\sqrt3}{2}\right)\left(-i\frac\pi3\right)\\ &=\frac\pi6\left(\sqrt3+i\right) \end{align} $$
Note on the log
Since $e^{i\pi/3}$ is on the unit circle at angle $\pi/3$, we have this diagram
$\hspace{3.8cm}$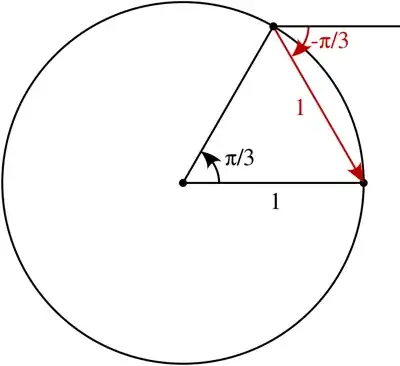
Thus, $\left|1-e^{i\pi/3}\right|=1$ and $\arg\left(1-e^{i\pi/3}\right)=-\pi/3$. Therefore, $$ \log\left(1-e^{i\pi/3}\right)=0-i\frac\pi3 $$
robjohn
- 345,667
-
1I think your omitted line are $$e^{i\phi}=\cos\phi+i\sin\phi, 1-e^{2yi}=1-\cos2y-i\sin2y=2\sin^2y-2i\sin y\cos y$$ $$=-2i\sin y(\cos y+i\sin y)\implies \ln(1-e^{2yi})=\ln2+\ln(-i)+\ln(\sin y)+iy$$ here $2y=\frac\pi3$ – lab bhattacharjee Feb 10 '14 at 18:39
-
1@labbhattacharjee: actually, I just drew the points $1$ and $e^{i\pi/3}$ and noted that because of the angle of $\pi/3$, they formed an equilateral triangle with the origin. This tells that $|1-e^{i\pi/3}|=1$ and $\mathrm{arg}(1-e^{i\pi/3})=-i\pi/3$. This tells that $\log(1-e^{i\pi/3})=-i\pi/3$. – robjohn Feb 10 '14 at 19:04
-