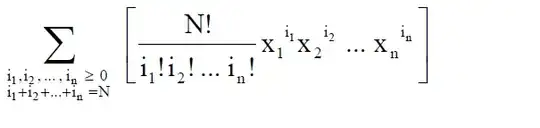I am reading about the multinomial theorem here
How do I read the summation notation in this line:
Also, can someone please show me how to apply it to the following expansion:
$$\left( x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}\right)^4$$
I am not sure how to map the notation into the actual expression.
The multinomial notation means that this is the sum over all possible values $i_1,i_2,\dots, i_n$ for which $i_1+i_2+\dots +i_n=N$ holds. This means that, for $n=2$ and $N=3$, you have the values $0,3$, $1,2$ $2,1$ and $3,0$, meaning that the sum in this case would contain the sumands $$\frac{3!}{3!0!}x_1^3x_2^0+\frac{3!}{2!1!}x_1^2x_2^1 + \frac{3!}{1!2!}x_1^1x_2^2+\frac{3!}{0!3!}x_1^0x_2^3. $$
In your case, you have $N=4$ and $n=4$, so you have some more combinations, namely $34$. This gives you $34$ different values to sum up. It's a mess, but doable.
The $34$ combinations are: $(4,0,0,0)$, $(0,4,0,0)$, $(0,0,4,0)$ and $(0,0,0,4)$ to begin with, then all possibilities of $4=3+1$, of which there are $12$:
$3,1,0,0$
$3,0,0,0$
$3,0,1,0$
$3,0,0,1$
$1,3,0,0$
$0,3,1,0$
$0,3,0,1$
$1,0,3,0$
$0,1,3,0$
$0,0,3,1$
$1,0,0,3$
$0,1,0,3$
$0,0,1,3$
then all possibilities for $4=2+1+1$, again there are $12$ of them:
$2,1,1,0$
$2,1,0,1$
$2,0,1,1$
$1,2,1,0$
$1,2,0,1$
$0,2,1,1$
$1,1,2,0$
$1,0,2,1$
$0,1,2,1$
$1,1,0,2$
$1,0,1,2$
$0,1,1,2$
and another $6$ possibilities for $4=2+2$:
$2,2,0,0$
$2,0,2,0$
$2,0,0,2$
$0,2,2,0$
$0,2,0,2$
$0,0,2,2$
Edit: One last possible way of writing $4$ as a sum of $4$ integers is of course $4=1+1+1+1$, yielding a total of $35$ possible ways.
There is no need to remember the formula. Its a consequence of simple combinatorics. I assume you know that if you are given $n_1$ objects of type $1$, $n_2$ objects of type $2$,... and $n_k$ objects of type $k$ with $n_1 + \dots n_k = N$, then there are $\frac{N !}{n_1 ! \dots n_k !}$ distinct arrangements.
The same happens when you consider $(x_1 + \dots x_k)^N$. Every term in its expansion is of degree $N$ and if you need to find the coefficient of say $x_1 ^{i_1} \dots x_k ^{i_k}$, the problem is equivalent to the above problem. Using the same argument we can write the given formula.
So, given $N$, find different partitions of $N$ and for each partition write the given formula.
I don't know if this is the simple way of understanding the multinomial formula. But here an algebric proof of it.
1-
Let's note $D(n;r)$ all the possible partition of $\left \{ 1;...;n \right \}$ indexes by $\left \{ 1;...;r \right \}$. That means all the possible partition of $\left \{ 1;...;n \right \}$ into $r$ subsets.
We can note that $D(n;r)= $ { The set of all partitions in $r$ sub sets such that the first sub set has $i_1$=1 element, the segond sub set has $i_2$=3 elements, ... the $l$-th subset has $i_l$ elements... such that of course $i_1+i_2+...+i_l+...=n$ } $\cup$ { The set of all partitions in $r$ sub sets such that the first sub set has $i_1$=4 element, the segond sub set has $i_2$=1 elements, ... the $l$-th subset has $i_l$ elements... such that of course $i_1+i_2+...+i_l+...=n$ } $\cup ...$
More generally we writte $D(n; i_1, i_2, ..., i_r)$ a possible partition of $\left \{ 1;...;n \right \}$ into $r$ sub set s.t. the first sub set has $i_1$ elements, the second $i_2$...and of course $i_1+i_2+...+i_l+...=n$.
Thus we get $D(n;r)=\bigcup_{all \, possibles \, (i_1;i_2;...;i_r) \in \mathbb{N} \, s.t. i_1+...+i_r=n }^{} D(n; i_1, ..., i_r)$. In other words we redescribe $D(n;r)$ as an union of smaller sub set $D(n; i_1, ..., i_r)$.
2-
Now let focus on $D(n; i_1, ..., i_r)$. From here we know that there is exactly $|D(n;i_1,...,i_r)| = \frac{n!}{i_1! i_2! ... i_n!}$ elements in each $D(n;i_1,...,i_r)$.
3-
By definition $(x_1+x_2+...+x_r)^n=$ the sum of all possibles multiplications that can be made by multipliying $n$ elements chosen (with or without repetition) from $ \left \{ x_1;x_2;...;x_r \right \} = $ sum on each of $D(n;r)$ partition possible where the power of an $ x_i \in \left \{ x_1;x_2;...;x_r \right \}$ is given by the number of elements in his correspondant sub set in the partition (maybe equal to $0$). Indeed the fact that we choose $n$ elements from $ \left \{ x_1;x_2;...;x_r \right \} $ caused that the total power on each element of this big sum, "sum up/is equal" to $n$.
But we gave in "-1" a complete disjoint descritption of $D(n;r)$ hence.
$(x_1+x_2+...+x_r)^n=\sum_{\pi \in D(n;r)}^{}x_1^{|\pi (index \, 1)|} \cdot ... \cdot x_r^{|\pi (index \, r)|}= \sum_{(i_1,...,i_n) \,s.t. \,i_1+...+i_n=n}^{}\binom{n}{i_1,i_2,...,i_r} x_1^{i_1} \cdot x_2^{i_2} \cdot ... \cdot x_r^{i_r}$
Where $ \pi $ is a specific partition of $D(n;r)$ and where, for exemple, $|\pi (index \, 1)|$ gives the number of element in the first intervall $I_1$ corresponding to $x_i$ in the given partition $\pi$. See here for more details with exemple.
Note that $|\pi ( index \, 1)| + ... + |\pi ( index \, r)| = n$
Q.E.D.
