Tangent line of a convex function

Question

Let $V : \mathbb{R}^n \rightarrow \mathbb{R}$ be (strictly) convex and continuously differentiable on $\mathbb{R}^n$. Show that for any $y \in \mathbb{R}^n$ and any $x \in \mathbb{R}^n$ $$ V(y) \geq V(x) + \nabla V(x)^\top(y-x) $$ For $n=1$ this implies that for any $x \in \mathbb{R}$ and for any $y \in \mathbb{R}$, $V(y)$ lies above the tangent line to $V$ at $x$.

Answer 1

$ \newcommand\R{\mathbb R} \newcommand\x{\mathbf x} \newcommand\y{\mathbf y} $Let $\gamma\colon\R\to\R^n$ be the curve defined by $t\mapsto \x+t(\y-\x)$, which is a straight line through $\gamma(0)=\x$ and $\gamma(1)=\y$. Further define $\widetilde V=V\circ \gamma:\R\to\R$.

Since $V\colon\R^n\to\R$ is differentiable, \begin{align} \nabla V(\x)\cdot (\y-\x) &= \lim_{h\to 0} \frac{V(\x+h(\y-\x))-V(\x)}{h} \\&= \lim_{h\to 0} \frac{V(\gamma(h))-V(\gamma(0))}{h} = \widetilde V'(0). \end{align}

Thus, your inequality can be expressed as $$ \widetilde V(1) \ge \widetilde V(0) + \widetilde V'(0). $$

It is easy to check that $\widetilde V$ is convex given that $V$ is convex.

After this, we have reduced everything to the claim foir $n=1$, $x=0$ and $y=1$.

Since $\widetilde V$ is convex, for all $t\in(0,1)$ we have $$ \widetilde V(t) \le (1-t) \widetilde V(0) + t\widetilde V(1) $$ which is equivalent to $$ \widetilde V(0) + \frac{\widetilde V(t)-\widetilde V(0)}{t} \le \widetilde V(1). $$ Letting $t\to 0$ gives the desired inequality.

Answer 2

I am well aware that the question is old and already has very good answers. But, since as in the linked duplicate question here someone might also care about the intuition on how to derive the proof and the other answers are more formal, let me just add some informal explanations together with some imaginery that visualize the relationship and build intuition in the one-dimensional case.

In my opinion, the underlying idea about the proof is the link between convexity of the function and the behavior of its derivatives. When you know that $f$ is convex, you know the derivative $f'$ is monotonically increasing. This is a standard textbook result. Now, the claim that the graph of a convex function always lies above the tangent line of any of its points, can be regarded as the statement that the graph curves away from the tangent line, positioning the graph of $f$ above it.

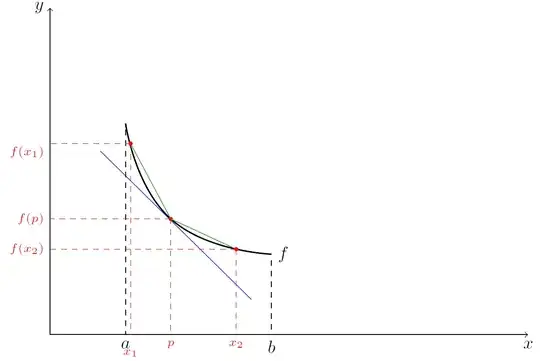
To see that relationship, consider the following graph I produced in TikZ.

We have to show the claim for arbitrary $x \in (a, b)$ and $p \in (a, b)$. Therefore, take some $p \in (a, b)$ like in the picture. First, we consider another point $x_2 \in (a, b)$ such that $x_2 > p$. We know that $f$ is convex. So, because it holds that $f'(p) < f'(x_2)$ since $p < x_2$ and $f'$ monotonically increasing due to its convexity, we have that \begin{equation} f'(x_2) \geq \frac{f(x_2) - f(p)}{x_2 - p} \geq f'(p) \end{equation} The middle term just represents the green secant line in the picture, between $p$ and $x_2$. The RHS inequality then immediately implies that $f(x_2) \geq f(p) + f'(p)(x_2 - p)$ and so the claim holds for all $x \in (p, b)$.

Now, what if we consider points $x$ for which $x < p$, i.e. $x \in (a, p)$? Take $x_1 \in (a, p)$ as in the picture. Then, we similarly have that \begin{equation} f'(p) \geq \frac{f(p) - f(x_1)}{p - x_1} \geq f'(x_1) \end{equation} again due to the monotone increase of $f'$ which is due to its convexity.

But then \begin{equation} f'(p) \geq \frac{f(p) - f(x_1)}{p - x_1} \iff f'(p) \geq \frac{(-1)}{(-1)}\frac{f(x_1) - f(p)}{x_1 - p} \iff f(p) + f'(p)(x_1 - p) \leq f(x_1) \end{equation} and voilà, we're done. Note that in the last step, the inequality sign changed because $x_1 - p < 0$.

Answer 3

This is true for any differentiable convex function. Let $f(t) = V(x + t (y-x))$ for $t \in [0,1]$.

First we establish an essentially equivalent (and fundamental) result that applies to all finite-valued convex functions: Suppose $x<y$, and let $R(x,y) = { f(x)-f(y) \over x-y }$. Then if $r < s<t$, we have $R(s,r) \le R(t,s)$.

To see this, note that if $s = \lambda t + (1-\lambda) r$, then $f(s) \le \lambda f(t) + (1-\lambda) f(r)$, or equivalently, $0 \le \lambda (f(t)-f(s)) + (1-\lambda) (f(r)-f(s))$. Since $\lambda = {s-r \over t-r}$ and $1-\lambda = { t-s \over t-r}$, substituting gives the result.

Now let $s = r+h$, where $0 < h < t-r$, then taking limits as $h \downarrow 0$ shows that $f'(r) \le R(t,r)$, or $f(t) \ge f(r) + f'(r) (t-r)$.

Choosing $t=1, r=0$ and noting that $f'(0) = \langle \nabla V(x), y-x \rangle$ yields the desired result.