What are examples of a basis of $C[0,1]$? (Hamel basis or Schauder basis... related: What is the difference between a Hamel basis and a Schauder basis?)
Asked
Active
Viewed 4,997 times
5
-
Do you mean as a vector space over $\mathbb{R}$ ? – WLOG Feb 07 '14 at 11:27
-
1The usual one is described here. Schauder discovered this basis, I believe; it is called the Schauder Basis of $C[0,1]$. – David Mitra Feb 07 '14 at 11:28
-
Related: http://math.stackexchange.com/questions/198575/explicit-norm-on-mathcalc0-mathbbr-mathbbr – Seirios Feb 07 '14 at 11:58
-
Do you mean a Hamel basis? – Matemáticos Chibchas Feb 07 '14 at 12:24
2 Answers
6
The Faber-Schauder basis of $C[0,1]$, mentioned by David Mitra, consists of the following functions: $f_0\equiv 1$, and after that $$f_{j,k} = (1-2^j|x-k/2^j|)^+,\quad j\ge 0, \quad 1\le k\le 2^j, \ \text{ $k$ is odd}$$ Apart from $f_0$, these are essentially antiderivatives of Rademacher functions, which hints at the reason for their good basis properties. The form a monotone Schauder basis for $C[0,1]$. In contrast, polynomials and trigonometric polynomials fail at this task.
A couple of pictures: functions up to $j=2$
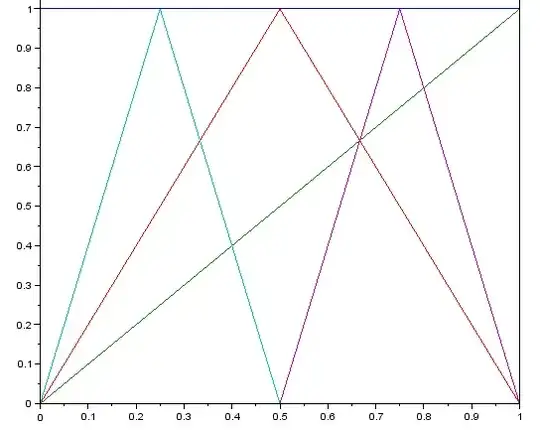
and up to $j=3$
hardmath
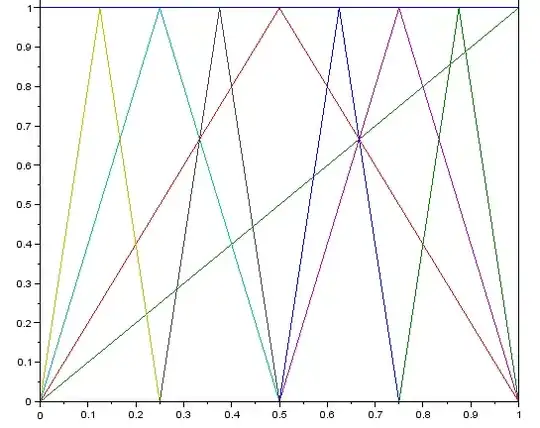
- 37,015
4
I assume you want Hamel basis. If you mean Schauder basis (or some other type of basis, like a base for the topology), you should say so.
I cannot write down a Hamel basis for $C[0,1]$. However, I can write down a linearly independent set of cardinal $\mathfrak{c} = 2^{\aleph_0}$. For $s \in (0,1)$, let $g_s \in C[0,1]$ be piecewise linear with $g_s(0)=0$, $g_s(1)=0$, $g_s(s) = 1$. The uncountable set $\{g_s : s \in (0,1) \}$ is linearly independent.
GEdgar
- 111,679