3

Prove that the foot of the perpendicular from the focus to any tangent of a parabola lies on the tangent to the vertex

I've been trying to prove this by plugging in the negative reciprocal of the slope of the tangent at a point $(x, y)$ into a line which passes through that point and the axis of symmetry. Then I plug the value of the focus into the result and solve for $x$. However the slope is undefined for any line parallel to the axis of symmetry.

Blue
  • 75,673
Tessera
  • 49

3 Answers3

5

Let $F$ be the focus of the parabola, $HG$ its directrix, with vertex $V$ the midpoint of $FH$. From the definition of parabola it follows that $PF=PG$, where $P$ is any point on the parabola and $G$ its projection on the directrix.

The tangent at $P$ is the angle bisector of $\angle FPG$, hence it is perpendicular to the base $GF$ of isosceles triangle $PFG$, and intersects it at its midpoint $M$.

But the tangent at $V$ is parallel to the directrix and bisects $FH$, hence it also bisects $FG$ at $M$, as it was to be proved.

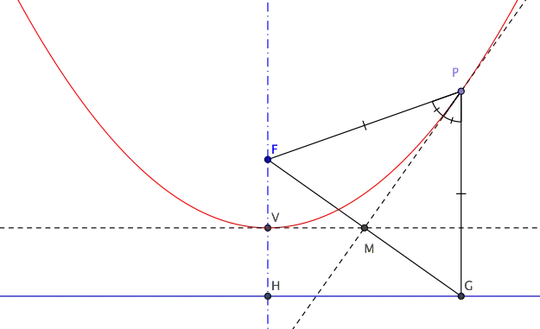
enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77
  • That the angle bisector $\angle FPG$ is tangent to the parabola at $P$ follows from the reflective property of parabolas. Indeed, a ray from $F$ to $P$ reflects vertically with the same angle on both sides of the tangent. – Rodrigo Dec 28 '20 at 14:00
  • This is the best answer – tryst with freedom Aug 05 '21 at 05:02
0

If you were to use a standard parabola like $y^2=4ax$, the usual way of representing a point on the parabola is via parametric equations $x=at^2$ and $y=2at$, so the general point is $(at^2, 2at)$.

The gradient of the tangent line to this point is thus $\frac{d(2at)} {dt}$ divided by $\frac{d(at^2)} {dt}$ i.e. $\frac{1}{t}$.

Thus the equation of the tangent line is $y=\frac{x} {t} + constant$ or $constant = ty - x$. We know the tangent line passes through $(at^2,2at)$, so substituting these values for $x$ and $y$ we get $constant= at^2$ and so the equation for our tangent is $$yt - x = at^2$$

The perpendicular through the focus must thus have gradient $-t$ and we know it passes through $(a,0)$. The equation of this line can be written $constant=y+tx$. Substituting $(a,0)$ for $(x,y)$ in this equation gives $constant=at$. Thus $$y+tx=at$$ is the equation of the perpendicular to the tangent through the focus.

Multiply both sides of this last equation by $t$ in order to eliminate terms in $y$ by subtracting the first equation to get $t^2x+x=0$, which can only be true if $x=0$. For $y^2=4ax$, $x=0$ is the equation of the vertex.

Gurnemanz
  • 21
0

Without loss of generality, we consider only the case $x^2=4ay$. the focus is $(0,a)$ and the slope at any point $(c,\frac{c^2}{4a})$ is $\frac{c}{2a}$ and the tangent equation is $$y-\frac{c^2}{4a}=\frac{c}{2a}(x-c)$$ Now you have to get the distance $d$ and find its minimum. $$d=\frac{4a(a)-2c(0)-c^2+2c^2}{\sqrt{16a^2+4c^2}} \\=\frac{4a^2+c^2}{\sqrt{16a^2+4c^2}} \\=\frac{1}{2}\sqrt{4a^2+c^2}$$ this distace has its minimum varying values of $c$ at $c=0$ and so $d=a$ I hope this helps

Semsem
  • 7,651